Challenge Math Challenge - May 2021

[fresh_42]

Summary: Group Theory, Integrals, Representation Theory, Iterations, Geometry, Abstract Algebra, Linear Algebra.1. Integrate
$$
\int_{0}^\infty \int_{0}^\infty e^{-\left(x+y+\frac{\lambda^3 }{xy}\right)} x^{-\frac{2}{3}}y^{-\frac{1}{3}}\,dx\,dy
$$

2. (solved by @Infrared , basic solution still possible ) Let $F_n$ be the free group of rank $n$ with generators $\{w_1,\ldots,w_n\}.$ Then
$$
\prod_{i=1}^m w_{a_i}^{b_i} \in [F_n,F_n] \Longleftrightarrow \forall_{k=1}^m \;\sum_{a_i=k}b_i =0
$$

3. (solved by @julian ) Calculate
$$
\int_0^\pi \int_0^\pi \int_0^\pi \dfrac{1}{1-\cos x\,\cos y\,\cos z}\,dx\,dy\,dz
$$

4. (solved by @fishturtle1 ) Let $G$ be a finite group, $\mathbb{K}$ a field such that $\operatorname{char}(\mathbb{K})\nmid |G|,$ and $(\rho,V)$ and $(\tau,W)$ linear representations of $G$ over $\mathbb{K}.$ The $\mathbb{K}-$linear mapping
\begin{align*}
\operatorname{Sym}\, : \,\operatorname{Hom}_\mathbb{K}(V,W)&\longrightarrow
\operatorname{Hom}_\mathbb{K}(V,W)\\
\varphi &\longmapsto \operatorname{Sym}(\varphi)=\dfrac{1}{|G|}\sum_{g\in G}\tau(g)\circ\varphi \circ\rho(g^{-1})
\end{align*}
is a projection onto the subspace
$$
\operatorname{Hom}_\mathbb{K}((\rho,V),(\tau,W))=\{\vartheta :V\longrightarrow W\,|\,\forall_{g\in G}\, : \,\tau(g)\circ\vartheta\circ \rho(g^{-1})=\vartheta \}
$$
of $\operatorname{Hom}_\mathbb{K}(V,W).$ Determine and prove (mention) all five claims.

5. Let $f(x)=x^3-\dfrac{49}{6}x^2+\dfrac{39}{2}x-\dfrac{31}{3}$. Prove that there are at least one $a,b$ such that $f^2(a)=a\, , \,f(a)\neq a$ and $f^4(b)=b\, , \,f^k(b)\neq b\;(k<4)$ where $f^n:=f\circ f^{n-1}, f^1=f.$
Is this true for every even power?

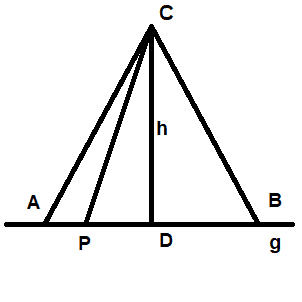
6. (solved by @etotheipi ) Prove the equivalence of the theorem of Pythagoras with the following transversal theorem about isosceles triangles:

Given an isosceles triangle $\triangle ABC$ with baseline $\overline{AB}\subseteq g,$ peak $C,$ i.e. $|AC|=|BC|,$ and $g$ the straight along the baseline. Moreover let $P\in g$ be an arbitrary point. Then
\begin{align*}
|CP|^{2}&=|CA|^{2}+|PA|\cdot |PB|\text{ if }P\not \in \overline{AB}\\
|CP|^{2}&=|CA|^{2}-|PA|\cdot |PB|\text{ if }P \in \overline{AB}
\end{align*}

7. (solved by @julian , another solution via MVT still possible ) Let $\alpha$ be an algebraic number of degree $n\geq 1.$ Then there is a real number $c>0$ such that for all $\mathbb{Q}\ni\dfrac{p}{q}\neq \alpha$
$$
\left|\alpha -\dfrac{p}{q}\right|\geq \dfrac{c}{q^n}
$$

8. (solved by @etotheipi ) Let $a_{n+1}=2+\sqrt{4+a_n}\, , \,a_0\geq -4\,,$ be a sequence of real numbers. Determine - if existent - its limit in dependence of the initial value $a_0,$ and show that $a_n\in [2,5]$ in cases where $a_0\in[-4,5],$ and $a_n\geq 5$ in cases where $a_0\geq 5$ $(n\in \mathbb{N}).$

9. (solved by @etotheipi ) Calculate center, foci, semi-axis, and area of the maximal inscribed ellipse of the triangle $(1,1),(5,2),(3,6).$

10. (solved by @julian ) Let $A,B\in \mathbb{M}(n,\mathbb{F})$ be two square $n\times n$ matrices over a field $\mathbb{F}.$ Show that the minimal polynomials of $AB$ and $BA$ are the same in case $A$ is regular. Is it true as well, if $A$ is singular?

High Schoolers only (until 26th)11. (solved by @kshitij ) For which positive real numbers $\mathbb{R}\ni a,b>0$ does
$$
f(a,b)=\dfrac{a^4}{b^4}+\dfrac{b^4}{a^4}-\dfrac{a^2}{b^2}-\dfrac{b^2}{a^2}+\dfrac{a}{b}+\dfrac{b}{a}
$$
assume a minimal value, and which one?

12. (solved by @kshitij ) Find all pairs $(x,y)$ of integers such that
$$
y^2=x\cdot (x+1)\cdot (x+7)\cdot (x+8)
$$

13. (solved by @kshitij ) Show that
$$
\underbrace{\left|x-\dfrac{\sin(x)(14+\cos(x))}{9+6\cos(x)}\right|}_{=:f(x)}\leq 10^{-4}\text{ for } x\in \left[0,\dfrac{\pi}{4}\right]
$$
You may use $\pi =3.14159+\delta \, , \,\sqrt{2}=1.41421+\varepsilon$ with $\delta,\varepsilon \in \left(0,10^{-5}\right).$

14. (solved by @kshitij ) If $f(x)=a_nx^n+\ldots+a_1x+a_0\in \mathbb{R}[x]$ is a real polynomial of degree $n$ which doesn't have real zeros, and $h\in\mathbb{R}$ a real number, then
$$
F(x):=f(x)+h\cdot f'(x)+h^2\cdot f''(x)+\ldots+h^n\cdot f^{(n)}(x)
$$
doesn't have real zeros either.

15. (solved by @kshitij ) Solve the following real equations system:
\begin{align*}
x+y&=az\\
x-y&=bz\\
x^2+y^2&=cz
\end{align*}

 

[etotheipi]

Problem 6. Let the angle $\angle CAB = \angle CBA := \theta$. First consider $P \in \overline{AB}$, then by the cosine rule $$|CP|^2 = |CA|^2 + |AP|^2 - 2|CA|\cdot|AP| \cos{\theta}$$Since $|AB| = 2|CA| \cos{\theta}$ then $$|AP|^2 - 2|CA| \cdot|AP| \cos{\theta} = |AP| \cdot\left( |AP| - 2 |CA| \cos{\theta} \right) = |AP|\cdot \left( |AP| - |AB| \right) = -|AP|\cdot |BP|$$hence $|CP|^2 = |CA|^2 - |AP|\cdot |BP|$.

It's similar for $P \not \in \overline{AB}$. WLOG take $P$ to be on the left of $A$. Then\begin{align*}

|CP|^2 &= |CA|^2 + |AP|^2 - 2|CA|\cdot |AP| \cos{(\pi - \theta)} \\

&= |CA|^2 + |AP|\cdot \left( |AP| + 2|CA| \cos{\theta} \right) \\

&= |CA|^2 + |AP|\cdot \left( |AP| + |AB| \right) \\

&= |CA|^2 + |AP| \cdot|PB|
\end{align*}

 

[etotheipi]

Wait - I didn't really read the question and at second glance I don't think that's what it's asking. And on that note, I don't actually know what it means to prove equivalence with Pythagoras...

 

[fresh_42]

It means the one implies the other and vice versa.

 

[etotheipi]

Oh, okay! In that case for the direction transversal $\implies$ Pythagoras you can just take $P = D$ (in which case $|BP| = |AP|$). For the converse, consider first $P \in \overline{AB}$. Then\begin{align*}
h^2 + |PD|^2 &= |CP|^2 \\
h^2 + |AD|^2 &= |CA|^2\end{align*}and so \begin{align*}

|CP|^2 &= |CA|^2 - (|AD|^2 - |PD|^2) \\

&= |CA|^2 - (|AD| + |PD|) \cdot (|AD| - |PD|) \\

&= |CA|^2 - |AP| \cdot |BP|

\end{align*}since $|AD| + |PD| = |BD| + |PD| = |BP|$ and also $|AD| - |PD| = |AP|$. You also take the exact same approach for when $P \not \in \overline{AB}$.

 

[julian]

#10

The minimal polynomial of $AB$ is the unique monic polynomial $p$ of smallest degree such that $p (AB) = 0$. Explicitly $p (AB) = 0$ reads:

$a_0 \mathbb{1} + a_1 AB + a_2 (AB)^2 + \cdots + (AB)^m = 0 \quad (*)$

Say $A$ is regular, multiplying from the left by $A^{-1}$ and from the right by $A$ gives

$a_0 \mathbb{1} + a_1 BA + a_2 (BA)^2 + \cdots + (BA)^m = 0 ,$

This is the smallest monic polynomial in $BA$ such that it is equal to zero. To prove this, suppose otherwise and assume that

$q (BA) = b_0 \mathbb{1} + b_1 BA + b_2 (BA)^2 + \cdots + (BA)^l = 0 \quad (**)$

where $l < m$. Multiplying $(**)$ from the left by $A$ and from the right with $A^{-1}$ would result in $q (AB) = 0$. A contradiction seeing as $(*)$ is the smallest monic polynomial in $AB$ that is equal to zero.

Is it not true as well, if $A$ is singular. Consider these two $n \times n$ matrices:

$A = \begin{pmatrix} 0 & \cdots & 1 \\ \vdots & & \vdots \\ 0 & \cdots & 0 \end{pmatrix} \quad B = \begin{pmatrix} 0 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & \cdots & 1 \end{pmatrix}$

Then

$AB = \begin{pmatrix} 0 & \cdots & 1 \\ \vdots & & \vdots \\ 0 & \cdots & 0 \end{pmatrix}$

whereas

$BA = \begin{pmatrix} 0 & \cdots & 0 \\ \vdots & & \vdots \\ 0 & \cdots & 0 \end{pmatrix}$

So $BA = 0$. We have that $(AB)^2 = 0$. So $BA$ has the minimal polynomial is $p (z) = z$. And $AB$ has the minimal polynomial is $p (z) = z^2$.

 

[etotheipi]

8. Let $a_{n+1}=2+\sqrt{4+a_n}\, , \,a_0\geq -4\,,$ be a sequence of real numbers. Determine - if existent - its limit in dependence of the initial value $a_0,$ and show that $a_n\in [2,5]$ in cases where $a_0\in[-4,5],$ and $a_n\geq 5$ in cases where $a_0\geq 5$ $(n\in \mathbb{N}).$

I'll try, I'm not so confident with these so some pointers would be appreciated. It is first worth to note that if $a_0 \geq -4$ then $a_1 \geq 2$. And if $a_k > 0$ then $a_{k+1} = 2 + \sqrt{4+ a_k} > 0$ so all the $a_k$ for $k > 0$ are positive. Now consider\begin{align*}

|a_{n} - 5| = |\sqrt{4+a_{n-1}} - 3| &= \left| \frac{(\sqrt{4+a_{n-1}} + 3)(\sqrt{4+a_{n-1}} - 3)}{(\sqrt{4+a_{n-1}} + 3)} \right| \\ \\

&= \left| \frac{a_{n-1} - 5}{\sqrt{4+a_{n-1}} + 3} \right| \\

&\leq \frac{1}{5} \left| a_{n-1} - 5 \right| \\

&\leq \dots \leq \frac{1}{5^{n-1}} \left| a_1 - 5 \right|

\end{align*}So given any $\epsilon > 0$ we can choose $N$ as any integer greater than $1 + \mathrm{log}_5 \frac{|a_1 - 5|}{\epsilon}$ in order to have $|a_n - 5| < \epsilon$ for all $n > N$, and the limit is hence $L = 5$ for $a_0 \in [-4, \infty)$.

For the last bit I suppose you can just say that if $a_0 \geq -4$ then $a_1 \geq 2$ and if $a_k \geq 2$ then $a_{k+1} = 2 + \sqrt{4+a_k} \geq 2$. Similarly, if $a_k < 5$ then $a_{k+1} = 2 + \sqrt{4 + a_k} < 2 + \sqrt{9} = 5$. So all the terms with $k > 0$ will satisfy $a_k \in [2,5)$.

And if $a_k \geq 5$ then $a_{k+1} = 2 + \sqrt{4 + a_k} \geq 2 + \sqrt{9} = 5$, so for $a_0 \geq 5$ you have $a_k \geq 5$ for all $k$.

Is it okay, or are there problems?

 

[fresh_42]

I'll try, I'm not so confident with these so some pointers would be appreciated. It is first worth to note that if $a_0 \geq -4$ then $a_1 \geq 2$. And if $a_k > 0$ then $a_{k+1} = 2 + \sqrt{4+ a_k} > 0$ so all the $a_k$ for $k > 0$ are positive. Now consider\begin{align*}

|a_{n} - 5| = |\sqrt{4+a_{n-1}} - 3| &= \left| \frac{(\sqrt{4+a_{n-1}} + 3)(\sqrt{4+a_{n-1}} - 3)}{(\sqrt{4+a_{n-1}} + 3)} \right| \\ \\

&= \left| \frac{a_{n-1} - 5}{\sqrt{4+a_{n-1}} + 3} \right| \\

&\leq \frac{1}{5} \left| a_{n-1} - 5 \right| \\

&\leq \dots \leq \frac{1}{5^{n-1}} \left| a_1 - 5 \right|

\end{align*}So given any $\epsilon > 0$ we can choose $N$ as any integer greater than $1 + \mathrm{log}_5 \frac{|a_1 - 5|}{\epsilon}$ in order to have $|a_n - 5| < \epsilon$ for all $n > N$, and the limit is hence $L = 5$ for $a_0 \in [-4, \infty)$.

For the last bit I suppose you can just say that if $a_0 \geq -4$ then $a_1 \geq 2$ and if $a_k \geq 2$ then $a_{k+1} = 2 + \sqrt{4+a_k} \geq 2$. Similarly, if $a_k < 5$ then $a_{k+1} = 2 + \sqrt{4 + a_k} < 2 + \sqrt{9} = 5$. So all the terms with $k > 0$ will satisfy $a_k \in [2,5)$.

And if $a_k \geq 5$ then $a_{k+1} = 2 + \sqrt{4 + a_k} \geq 2 + \sqrt{9} = 5$, so for $a_0 \geq 5$ you have $a_k \geq 5$ for all $k$.

Is it okay, or are there problems?

Well, a bit sloppy a.u. The proof about the ranges would have required a monotony argument and/or an induction, and for the question about the fixed point, a consideration about uniqueness would have been nice.

 

[romsofia]

Some idea on #8...

Spoiler

$\int_{0}^{\pi} \frac{1}{1-\cos x} \rightarrow \int_{0}^{\pi}\frac{1+\cos x}{1-\cos^2 x} \rightarrow \int_{0}^{\pi} \csc^2 x + \frac{\cos x}{\sin^2 x}$ Which looks like it diverges, so if it's not suppose to diverge, this would be the wrong way to go about it

 

[Office_Shredder]

For #10, I'm confused why you specified that A is regular, it seems like the solution just uses that it's invertible. Are those the same thing?

 

[fresh_42]

For #10, I'm confused why you specified that A is regular, it seems like the solution just uses that it's invertible. Are those the same thing?

It's the same in the finite-dimensional case. I have not really an idea about minimal polynomials and other properties in the infinite-dimensional case. Here it is bijective = isomorphism = invertible = non-singular = regular. At least I have learned it as such.

 

[etotheipi]

I was just playing around with number 9, I think if you subject the points to the following affine transformations:

- translate by $(-1,-1)$
- then rotate by $\frac{1}{\sqrt{17}}\begin{pmatrix} 4 & 1 \\ -1 & 4 \end{pmatrix}$
- then shear by $\begin{pmatrix} 1 & \frac{-1}{4} \\ 0 & 1 \end{pmatrix}$
- then stretch by $\begin{pmatrix} 1 & 0 \\ 0 & \frac{17\sqrt{3}}{36} \end{pmatrix}$

then you end up with an equilateral triangle with vertices $\mathcal{V} \in \{ (0,0), (\sqrt{17},0), (\sqrt{17}/2, \sqrt{51}/2) \}$. The overall affine transformation is$$\begin{pmatrix} X \\ Y \end{pmatrix} = \begin{pmatrix} \frac{\sqrt{17}}{4} & 0 \\ \frac{-\sqrt{17}}{12\sqrt{3}} & \frac{\sqrt{17}}{3\sqrt{3}} \end{pmatrix} \begin{pmatrix} x-1 \\ y-1 \end{pmatrix}$$In the resulting equilateral triangle the maximal inscribed ellipse is just a circle of centre $\mathbf{R}_C = (\sqrt{17}/2, \sqrt{51}/ 6)$ and radius $\mathscr{R} = \sqrt{51}/6$. The area of the original ellipse should simply scale as $A_{\mathrm{ellipse}} = (\mathrm{det} \mathcal{M}^{-1})^2 A_{\mathrm{circle}} = \frac{1}{(\mathrm{det} \mathcal{M})^2} A_{\mathrm{circle}}$.

Also, the circle has equation $\left(X - \frac{\sqrt{17}}{2} \right)^2 + \left(Y - \frac{\sqrt{51}}{6} \right)^2 = \frac{51}{36}$, so we can just substitute in for $X(x,y)$ and $Y(x,y)$ to find the equation of the ellipse.

I'm a bit tired to do remainder of the algebra now, though!

 

[fresh_42]

I want to see the center coordinates (up to 2 digits), foci coordinates (up to 2 digits), semi-axis (exact), area (exact). I need them to check whether it makes sense to read anything. No translated, rotated, or otherwise manipulated orbit equations. I am too lazy to decode the information from implicitly given equations.

 

[Infrared]

$\int_{0}^{\pi} \frac{1}{1-\cos x} \rightarrow \int_{0}^{\pi}\frac{1+\cos x}{1-\cos^2 x} \rightarrow \int_{0}^{\pi} \csc^2 x + \frac{\cos x}{\sin^2 x}$ Which looks like it diverges, so if it's not suppose to diverge, this would be the wrong way to go about it

Your integral diverges but the integral in the problem converges. A similar example is that $\int_0^1\frac{1}{x^2}dx$ diverges but $\iiint_{x^2+y^2+z^2\leq 1}\frac{1}{x^2+y^2+z^2}dx dy dz$ converges (use spherical coordinates).

 

[etotheipi]

I want to see the center coordinates (up to 2 digits), foci coordinates (up to 2 digits), semi-axis (exact), area (exact). I need them to check whether it makes sense to read anything. No translated, rotated, or otherwise manipulated orbit equations. I am too lazy to decode the information from implicitly given equations.

That said... my ellipse is:$$F(x,y) := \frac{119}{108}x^2 -\frac{17}{54} xy + \frac{17}{27}y^2 -\frac{17}{3}x - \frac{17}{6}y + \frac{34}{3} = 0$$the centre can be found either by the inverse affine map from in #12 or simply by setting $\nabla F(x_c, y_c) = 0$ which gives $(x_c, y_c) = (3,3)$. Is that what you got, as a start?

 

[fresh_42]

I haven't calculated the ellipse. The center is $(3,3)$, yes.

 

[etotheipi]

I have for the semi-major, semi-minor and area:\begin{align*}

a &= \frac{\sqrt{2}(11+ \sqrt{13})\sqrt{11-\sqrt{13}}}{36} \\

b &= \frac{\sqrt{2}(11- \sqrt{13})\sqrt{11+\sqrt{13}}}{36} \\

A_{\mathrm{ellipse}} &= \pi ab\end{align*}the centre-to-focus length is $c = \sqrt{a^2 - b^2}$. The focal points are then the $(x_{f\pm}, y_{f\pm}) = (3 \pm c\cos{\theta}, 3 \pm c\sin{\theta})$ where $\cos{\theta}$ and $\sin{\theta}$ satisfy\begin{align*}

\frac{119}{108} &= a^2 \sin^2{\theta} + b^2\cos^2{\theta} = (a^2 - b^2)\sin^2{\theta} + b^2

\end{align*}which could be found with a calculator, I guess

 

[etotheipi]

Do you have any hints for the integral in problem 3? I could only tell so far that with $x \mapsto u(x) = \pi - x$ you see $\mathcal{I} = \int_{\mathcal{D}} \frac{\mathrm{d}^3 x}{1-c(x)c(y)c(z) } = \int_{\mathcal{D}} \frac{\mathrm{d}^3 x}{1+c(x)c(y)c(z) } = \int_{\mathcal{D}} \frac{\mathrm{d}^3 x}{1-c(x)^2c(y)^2c(z)^2 }$...

 

[fresh_42]

I have for the semi-major, semi-minor and area:\begin{align*}

a &= \frac{\sqrt{2}(11+ \sqrt{13})\sqrt{11-\sqrt{13}}}{36} \\

b &= \frac{\sqrt{2}(11- \sqrt{13})\sqrt{11+\sqrt{13}}}{36} \\

A_{\mathrm{ellipse}} &= \pi ab\end{align*}the centre-to-focus length is $c = \sqrt{a^2 - b^2}$. The focal points are then the $(x_{f\pm}, y_{f\pm}) = (3 \pm c\cos{\theta}, 3 \pm c\sin{\theta})$ where $\cos{\theta}$ and $\sin{\theta}$ satisfy\begin{align*}

\frac{119}{108} &= a^2 \sin^2{\theta} + b^2\cos^2{\theta} = (a^2 - b^2)\sin^2{\theta} + b^2

\end{align*}which could be found with a calculator, I guess

I have different values, e.g. no $\sqrt{13}.$ And the area is a nice number, not a monster. You still deliver implicit solutions, instead of good old digits. However, I used a different method for calculation, so it's hard to compare them, especially as you didn't post what you had done exactly. E.g. the optimization process remains in the dark.

 

[fresh_42]

Do you have any hints for the integral in problem 3? I could only tell so far that with $x \mapsto u(x) = \pi - x$ you see $\mathcal{I} = \int_{\mathcal{D}} \frac{\mathrm{d}^3 x}{1-c(x)c(y)c(z) } = \int_{\mathcal{D}} \frac{\mathrm{d}^3 x}{1+c(x)c(y)c(z) } = \int_{\mathcal{D}} \frac{\mathrm{d}^3 x}{1-c(x)^2c(y)^2c(z)^2 }$...

@Infrared already gave a hint. Weierstraß is another.

 

[etotheipi]

And the area is a nice number, not a monster.

When I simplified my expression for $A_{\mathrm{ellipse}}$ using the exact expressions for $a \sim 1.56$ and $b \sim 1.11$ in post #19 I get $A_{\mathrm{ellipse}} = \pi\sqrt{3}$. I didn't calculate the focal coordinates exactly but I have $\boldsymbol{f}_{+} \sim (3.32, 4.05)$ and $\boldsymbol{f}_{-} \sim (2.68, 1.95)$

 

[etotheipi]

@Infrared already gave a hint. Weierstraß is another.

Hmm, okay I still don't know so I'll wait and see how someone else solves it! Weierstrass takes it to $\mathcal{I} = 4\int_{\mathcal{D}'} (t^2u^2v^2 + t^2 + u^2 + v^2)^{-1} \, \mathrm{d} t \, \mathrm{d}u \, \mathrm{d}v$ with $\mathcal{D}' = (0, \infty)^{3}$ but it also looks difficult to solve.

 

[fresh_42]

When I simplified my expression for $A_{\mathrm{ellipse}}$ using the exact expressions for $a \sim 1.56$ and $b \sim 1.11$ in post #19 I get $A_{\mathrm{ellipse}} = \sqrt{3}$. I didn't calculate the focal coordinates exactly but I have $\boldsymbol{f}_{+} \sim (3.32, 4.05)$ and $\boldsymbol{f}_{-} \sim (2.68, 1.95)$

You drive me crazy: sloppy a.u.! You dropped the $\pi$ in the area. The numbers are correct, except that I haven't checked $a,b$. Anyway, since we now have a collection of posts with partial solutions, I will post mine for the sake of completeness, and in case someone wants to learn about the Steiner ellipse:

Set
\begin{align*}
\mathbb{C}[x]\ni p(z)&=(z-1-i)(z-5-2i)(z-3-6i)\\&=z^3 - (9 + 9 i) z^2 + (3 + 52 i) z + (33 - 39 i)
\end{align*}
The maximal inscribed ellipse of the triangle of zeros of $p(x)$ is thus the Steiner inellipse, where the sides of the triangle are tangents at their midpoints. The foci are the zeros of $p'(z)$ and the center the zero of $p''(x)$ by Marden's theorem.
\begin{align*}
0&=p'(z)=3 z^2 - (18 + 18 i) z + (3 + 52 i)\\
&=3\left(z- (3 + 3 i) - \sqrt{-1+\dfrac{2i}{3}}\right)\left(z- (3 + 3 i)+\sqrt{-1+\dfrac{2i}{3}}\right)\\
&\approx 3\left(z-3.32-4.05 i \right)\left(z-2.68 - 1.95 i \right)\\
0&=p''(x)=6\left(z-(3+3i)\right)
\end{align*}
Hence the center of the ellipse is $(3,3)$ and the foci $(2.68,1.95),(3.32,4.05).$ The area of an ellipse is given as $A=\pi ab ,$ so we have to compute the semi-axis of a Steiner inellipse within $\triangle ABC$ with center $S.$
\begin{align*}
A=(1,1)\, , \,B=(5,2)\, &, \,C=(3,6)\, , \,S=(3,3)\, , \,\\
M:=\dfrac{1}{4}\left(\overline{SC}^2+\dfrac{1}{3}\overline{AB}^2\right)\, &, \,N:=\dfrac{1}{4\sqrt{3}}\cdot \left|\det\left(\vec{SC},\vec{AB}\right)\right|\\
a=\dfrac{1}{2}\left(\sqrt{M+2N}+\sqrt{M-2N}\right)\, &, \,b=\dfrac{1}{2}\left(\sqrt{M+2N}-\sqrt{M-2N}\right)
\end{align*}
\begin{align*}
M&=\dfrac{1}{4}\left(9+\dfrac{1}{3}\cdot 17\right)=\dfrac{11}{3}\\
N&=\dfrac{1}{4\sqrt{3}}\left|\det\left(\begin{bmatrix}
0&4\\3&1\end{bmatrix}\right)\right|=\sqrt{3}\\
a&=\dfrac{1}{2\sqrt{3}}\left(\sqrt{11+6\sqrt{3}}+\sqrt{11-6\sqrt{3}}\right)\\
b&=\dfrac{1}{2\sqrt{3}}\left(\sqrt{11+6\sqrt{3}}-\sqrt{11-6\sqrt{3}}\right)\\
ab&=\dfrac{1}{12}\left(\left(11+6\sqrt{3}\right)-\left(11-6\sqrt{3}\right)\right)=\sqrt{3}\\
A&=\pi\sqrt{3}\approx 5.44 \quad =\dfrac{\pi}{3\sqrt{3}}\cdot A_\triangle
\end{align*}

 

[benorin]

@fresh_42 does the answer to #1) involves $\Gamma \left( \tfrac{7}{3}\right)$? I got that times a divergent integral but the calculus I did was slapdash, just want to know if I’m out on the correct limb here.

 

[fresh_42]

@fresh_42 does the answer to #1) involves $\Gamma \left( \tfrac{7}{3}\right)$? I got that times a divergent integral but the calculus I did was slapdash, just want to know if I’m out on the correct limb here.

I have $1$ and $2$ as numerator, not $7$, hence the answer is maybe.

 

[Fred Wright]

Problem 1.

We have,
$$

I=\int_0^{\infty}\int_0^{\infty}e^{-(x+y+\frac{\lambda^3}{xy})}x^{-\frac{2}{3}}y^{-\frac{1}{3}}dxdy
$$
Make the following expansion under the integral sign,
$$

e^{-\frac{\lambda^3}{xy}}=\sum_{n=0}^{\infty}(\frac{\lambda^3}{xy})^n\frac{(-1)^n}{n!}
$$
to get
$$
I=\int_0^{\infty}e^{-y}y^{-\frac{1}{3}}\int_0^{\infty}e^{-x}x^{-\frac{2}{3}}(\sum_{n=0}^{\infty}(\frac{\lambda^3}{xy})^n\frac{(-1)^n}{n!})dxdy
$$
$$
=\int_0^{\infty}e^{-y}y^{-\frac{1}{3}}\sum_{n=0}^{\infty}(\int_0^{\infty}(-1)^n(\frac{\lambda^3}{y})^n\frac{x^{-n-\frac{2}{3}}}{n!}e^{-x}dx)dy\\
$$
Each x integral term in the expansion results in a Gamma function and taking the sum out side the remaining integral we get,
$$
I=\sum_{n=0}^{\infty}(-1)^n\lambda^{3n}\frac{\Gamma (\frac{1}{3}-n)}{n!}\int_0^{\infty}e^{-y}y^{-n-\frac{1}{3}}dy
$$
Again each term y integral term in the expansion results in a Gamma function.
$$
I=\sum_{n=0}^{\infty}(-1)^n\lambda^{3n}\Gamma (\frac{2}{3}-n)\frac{\Gamma (\frac{1}{3}-n)}{n!}
$$
By iterating each term in the sum using the identity,
$$
\Gamma (n-1)=\frac{\Gamma (n)}{n-1}
$$
we find,
$$

I=1+\sum_{n=1}^{\infty}(-1)^n\frac{\lambda^{3n}3^{2n}\Gamma (\frac{1}{3}) \Gamma (\frac{2}{3}) }{\Pi_{k=1}^n (3k-1) \Pi_{k=1}^n (3k-2)n!}
$$
Let $x=3\lambda$. On expanding each term in the sum we find,
$$I=\Gamma (\frac{1}{3})\Gamma (\frac{2}{3})\sum_{n=0}^{\infty}(-1)^n\frac{x^{3n}}{(3n)!}
$$
Let us seek a solution for $y(x)=\sum_{n=0}^{\infty}(-1)^n\frac{x^{3n}}{(3n)!}$ in the form of a second order differential equation. On expanding each term we have,
$$
y(x)= 1-\frac{x^3}{3!}+\frac{x^6}{6!}-\frac{x^9}{9!}+...
$$
$$
y'(x)=-\frac{x^2}{2!}+\frac{x^5}{5!}-\frac{x^8}{8!}+...
$$
$$
y''(x)=-x+\frac{x^4}{4!}-\frac{x^7}{7!}+\frac{x^{10}}{10!}-\frac{x^{13}}{13!}+...
$$
We observe,
$$
y''-y'+y=e^{-x}
$$
The characteristic polynomial for the homogeneous solution is,
$$
\lambda^2-\lambda + 1=0\\
$$
and thus,
$$
\lambda=\frac{1}{2}\pm \frac{i\sqrt{3}}{2}\\
$$
with the homogeneous solution,
$$
y_h(x)=e^{\frac{x}{2}}[c_1\cos(\frac{\sqrt{3}x}{2})+c_2\sin(\frac{\sqrt{3}x}{2})]
$$
The particular solution is of the form,
$$
y_p=Ce^{-x}
$$
Plugging this into the differential equation we find $C=\frac{1}{3}$. The solution is the sum of the homogeneous part and the particular part,
$$
y(x)=y_h(x)+y_p(x)
$$
Applying the boundary conditions $y(0)=1$ and $y'(0)=0$ we find $c_1=\frac{2}{3}$ and $c_2=0$. Thus
$$
y(x)=\frac{2}{3}e^{\frac{x}{2}}\cos(\frac{\sqrt{3}x}{2})+ \frac{1}{3}e^{-x}
$$
and we finally have,
$$
\int_0^{\infty}\int_0^{\infty}e^{-(x+y+\frac{\lambda^3}{xy})}x^{-\frac{2}{3}}y^{-\frac{1}{3}}dxdy=\Gamma (\frac{1}{3})\Gamma (\frac{2}{3})[\frac{2}{3}e^{\frac{(3\lambda)}{2}}\cos(\frac{3\sqrt{3}\lambda}{2})+ \frac{1}{3}e^{-3\lambda}]$$

 

[fresh_42]

Problem 1.

We have,
$$

I=\int_0^{\infty}\int_0^{\infty}e^{-(x+y+\frac{\lambda^3}{xy})}x^{-\frac{2}{3}}y^{-\frac{1}{3}}dxdy
$$
Make the following expansion under the integral sign,
$$

e^{-\frac{\lambda^3}{xy}}=\sum_{n=0}^{\infty}(\frac{\lambda^3}{xy})^n\frac{(-1)^n}{n!}
$$
to get
$$
I=\int_0^{\infty}e^{-y}y^{-\frac{1}{3}}\int_0^{\infty}e^{-x}x^{-\frac{2}{3}}(\sum_{n=0}^{\infty}(\frac{\lambda^3}{xy})^n\frac{(-1)^n}{n!})dxdy
$$
$$
=\int_0^{\infty}e^{-y}y^{-\frac{1}{3}}\sum_{n=0}^{\infty}(\int_0^{\infty}(-1)^n(\frac{\lambda^3}{y})^n\frac{x^{-n-\frac{2}{3}}}{n!}e^{-x}dx)dy\\
$$
Each x integral term in the expansion results in a Gamma function and taking the sum out side the remaining integral we get,
$$
I=\sum_{n=0}^{\infty}(-1)^n\lambda^{3n}\frac{\Gamma (\frac{1}{3}-n)}{n!}\int_0^{\infty}e^{-y}y^{-n-\frac{1}{3}}dy
$$
Again each term y integral term in the expansion results in a Gamma function.
$$
I=\sum_{n=0}^{\infty}(-1)^n\lambda^{3n}\Gamma (\frac{2}{3}-n)\frac{\Gamma (\frac{1}{3}-n)}{n!}
$$
By iterating each term in the sum using the identity,
$$
\Gamma (n-1)=\frac{\Gamma (n)}{n-1}
$$
we find,
$$

I=1+\sum_{n=1}^{\infty}(-1)^n\frac{\lambda^{3n}3^{2n}\Gamma (\frac{1}{3}) \Gamma (\frac{2}{3}) }{\Pi_{k=1}^n (3k-1) \Pi_{k=1}^n (3k-2)n!}
$$
Let $x=3\lambda$. On expanding each term in the sum we find,
$$I=\Gamma (\frac{1}{3})\Gamma (\frac{2}{3})\sum_{n=0}^{\infty}(-1)^n\frac{x^{3n}}{(3n)!}
$$
Let us seek a solution for $y(x)=\sum_{n=0}^{\infty}(-1)^n\frac{x^{3n}}{(3n)!}$ in the form of a second order differential equation. On expanding each term we have,
$$
y(x)= 1-\frac{x^3}{3!}+\frac{x^6}{6!}-\frac{x^9}{9!}+...
$$
$$
y'(x)=-\frac{x^2}{2!}+\frac{x^5}{5!}-\frac{x^8}{8!}+...
$$
$$
y''(x)=-x+\frac{x^4}{4!}-\frac{x^7}{7!}+\frac{x^{10}}{10!}-\frac{x^{13}}{13!}+...
$$
We observe,
$$
y''-y'+y=e^{-x}
$$
The characteristic polynomial for the homogeneous solution is,
$$
\lambda^2-\lambda + 1=0\\
$$
and thus,
$$
\lambda=\frac{1}{2}\pm \frac{i\sqrt{3}}{2}\\
$$
with the homogeneous solution,
$$
y_h(x)=e^{\frac{x}{2}}[c_1\cos(\frac{\sqrt{3}x}{2})+c_2\sin(\frac{\sqrt{3}x}{2})]
$$
The particular solution is of the form,
$$
y_p=Ce^{-x}
$$
Plugging this into the differential equation we find $C=\frac{1}{3}$. The solution is the sum of the homogeneous part and the particular part,
$$
y(x)=y_h(x)+y_p(x)
$$
Applying the boundary conditions $y(0)=1$ and $y'(0)=0$ we find $c_1=\frac{2}{3}$ and $c_2=0$. Thus
$$
y(x)=\frac{2}{3}e^{\frac{x}{2}}\cos(\frac{\sqrt{3}x}{2})+ \frac{1}{3}e^{-x}
$$
and we finally have,
$$
\int_0^{\infty}\int_0^{\infty}e^{-(x+y+\frac{\lambda^3}{xy})}x^{-\frac{2}{3}}y^{-\frac{1}{3}}dxdy=\Gamma (\frac{1}{3})\Gamma (\frac{2}{3})[\frac{2}{3}e^{\frac{(3\lambda)}{2}}\cos(\frac{3\sqrt{3}\lambda}{2})+ \frac{1}{3}e^{-3\lambda}]$$

Can you simplify this expression? A lot! Will say: 1 $e$, 1 $\pi$ , 1 $\lambda$, 1 $\sqrt{{}}$, 0 $\Gamma$ I think you made a mistake. My integral is far easier. The cosine term appears to be wrong.

 

[benorin]

Damn I was working integral transformations not series expansions. I shouldn’t have put my pencil down!

 

[fresh_42]

Damn I was working integral transformations not series expansions. I shouldn’t have put my pencil down!

That is my approach, too. The series solution seems to have a mistake somewhere. There is a useful trick to solve the integral quite easily.

 

[benorin]

I get

$$I=36\sum_{k=0}^\infty (-1)^k\tfrac{\lambda ^{3k}}{(3k-1)(3k-2)}$$

as a series solution for the integral using integral transformations and series expansions and Beta functions to finish it off.