alice22
- 35
- 0
Use English to explain what this is showing.
Also prove it!
alice22 said: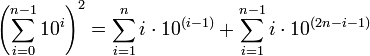
Use English to explain what this is showing.
Also prove it!
alice22 said: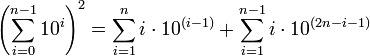
Use English to explain what this is showing.
Also prove it!
HallsofIvy said:The simplest thing to do is to look at what it says for some small n- say n= 3.
\left(\sum_{i=0}^{3-1}10^i\right)^2= \left(10^0+ 10^1+ 10^2\right)^2= (1+ 10+ 100)^2= 111^2.
\sum_{i=1}^n i10^{i-1}= 1(10^0)+ 2(10^1)+ 3(10^2)= 321
\sum_{i=1}^{n-1} i10^{2n-i-1}= 1(10^4}+ 2(10^3)= 1200
It's easy to calculate that 111^2= 12321= 1200+ 321.
11^2= 121, 111^3= 12321, 1111^2= 1234321 , etc.
Do you see the pattern?
\sum_{i=1}^{n-1} i10^{2n-i-1}
is the first part- the 1234... Do you see how it is counting "down" because of the 10^{2n-i-1}?
\sum_{i=1}^n i10^{i-1}
is the last part: 321