MATLAB Center Wavelength of Fiber Bragg Grating Filter

In summary, the conversation discusses the difficulty of locating the center wavelength of a FBG notch filter in MATLAB. The speaker has tried using a quadratic fit, but it is dependent on the amount of data points and does not accurately locate the peak. They are seeking help and clarification on the 10 data points mentioned and their relevance to the task.
  • #1
spyrius
1
0
I would like to locate the center wavelength of a FBG notch filter in MATLAB, but I'm having trouble getting an answer within 0.01nm of the correct wavelength.

upload_2016-2-16_20-55-55.png
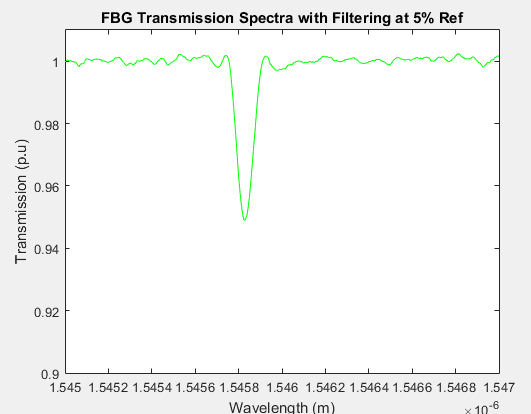So far I've tried using a quadratic fit with MATLAB, but that is too dependent on the amount of data points to the left and right of the notch. The location of the peak is also not correct, because the filter is only made up of ~10 discrete data points, and the highest/lowest one is not necessarily the center.

Any help would be appreciated.
 
  • #3
Can you fill us in a bit more on what you're trying to do? Are the 10 points you mentioned points taken from the graph you showed? If so, it's entirely possible that with such a small data set, you could completely miss the valley (it's not a peak) at 1.5458 ##\mu##m.
 

1. What is a Fiber Bragg Grating (FBG) Filter?

A Fiber Bragg Grating (FBG) Filter is a type of optical filter that is used in fiber optic communication systems to selectively reflect specific wavelengths of light while allowing other wavelengths to pass through. It is made up of a periodic variation in the refractive index of the fiber core, which acts as a wavelength selective mirror.

2. What is the MATLAB Center Wavelength of a FBG Filter?

The MATLAB Center Wavelength of a FBG Filter refers to the wavelength at which the filter reflects the most light. This is typically the center of the stop band, where the filter's reflectance is at its highest. It can be calculated using MATLAB software by analyzing the filter's transmission spectrum.

3. How is the Center Wavelength of a FBG Filter measured?

The Center Wavelength of a FBG Filter is typically measured using an optical spectrum analyzer, which measures the filter's transmission spectrum. The center wavelength can then be determined by finding the peak of the filter's reflectance curve.

4. What factors affect the Center Wavelength of a FBG Filter?

The Center Wavelength of a FBG Filter can be affected by various factors such as the grating period, the refractive index modulation, and the temperature. Any changes in these parameters can cause a shift in the center wavelength, which can be compensated for by adjusting the filter's design or using temperature control techniques.

5. What is the importance of the Center Wavelength in a FBG Filter?

The Center Wavelength of a FBG Filter is crucial in determining the filter's performance and its ability to selectively reflect specific wavelengths of light. It is also used to calibrate and tune the filter for specific applications and to ensure its stability over time. Accurate measurement and control of the center wavelength is essential for reliable and efficient operation of fiber optic communication systems.

Similar threads

FBG Wavelength Reflection in Double-Clad MMF for 910 nm Laser Diode
    • Other Physics Topics
Replies
1
Views
1K
Engineering Statics 3D equilibrium (sleeves and ball joints)
    • Engineering and Comp Sci Homework Help
Replies
2
Views
4K
Distributed Strain Sensing with FO Bragg Gratings
    • Mechanical Engineering
Replies
1
Views
2K
B Infrared Detectors & The 2nd Law of Thermodynamics
    • Thermodynamics
5
Replies
152
Views
5K
Understanding Photon Absorption in Radio Wavelengths: 3 Key Questions Explored
    • Quantum Physics
2
Replies
43
Views
3K
What kind of filters to use for audio LED spectrum analyzer?
    • Electrical Engineering
Replies
15
Views
8K
Loop-de-Loop with function of angle
    • Introductory Physics Homework Help
Replies
25
Views
3K
Birefringence and Automotive Window Tinting
    • Classical Physics
Replies
9
Views
6K
A Schrödinger's original interpretation
    • Quantum Interpretations and Foundations
Replies
21
Views
2K
Programs How good is this applied math program?
    • STEM Academic Advising
Replies
13
Views
2K

Hot Threads

Recent Insights

Back
Top