Matrix of rotated elements (stiffness matrix)

[Amaelle]

Good day All
I have a doubt regarding the derivation of the following matrix

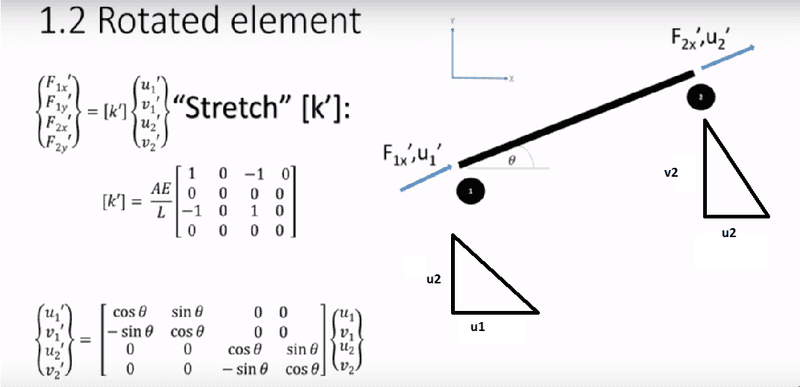
according to my basic understanding we want to go from the basis u1 v1 u2 v2 to the basis u'1 v'1 u'2 v'2, and for doing so we use the rotation matrix

the rotation matrix is the following and the angle theta is positive

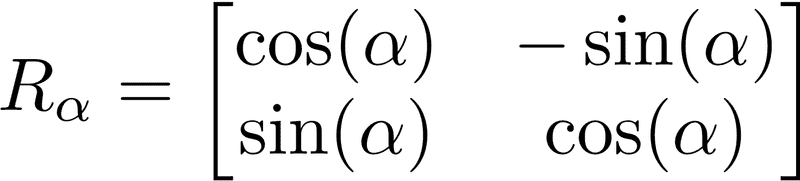
but i still can 't understand why the signs are inverted?
any help would be highly appreciated
Many thanks in advance!

 

[StoneTemplePython]

I'm not sure what the "stretch k" and some other symbols on here are referring to, but you may consider what happens if you multiply each side by the transpose of your matrix. Transposition 'flips' the negative signs that seem out of place here. The matrix is orthogonal, so you may just be missing which matrix is the "original one" and which one is the inverse.

 

[Amaelle]

I'm not sure what the "stretch k" and some other symbols on here are referring to, but you may consider what happens if you multiply each side by the transpose of your matrix. Transposition 'flips' the negative signs that seem out of place here. The matrix is orthogonal, so you may just be missing which matrix is the "original one" and which one is the inverse.

Thanks a lot!