Maximizing x-component of force

[Physics2341313]

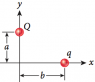
A charge Q is placed at a distance a = 3m and a charge q is placed at a distance b

For what value(s) of b is the x-component of the force maximized?

I know to maximize the force we need to maximize F_Qq = k Qq b/(3^2 + b^2)^{3/2}.

To do this we need to set the first derivative to zero and solve for b. Can someone walk me through this derivative? Having trouble with this and I can't seem to get it. The b in the numerator and 3/2 power came from taking the unit vector.

kQq are just constants so we just need to take the derivative of b/(9 + b^2)^{3/2} no?

 

[rude man]

Need picture.

 

[Physics2341313]

Here's the picture of the figure, where a = 3m in this specific case. I guess I should have also stated that the b in the numerator and the 3/2 power came from the cosine to be more correct in terminology?

 

[rude man]

x component of the force on which charge?
what are the signs of the charges? both +? both -? one each?

 

[Physics2341313]

x-component on q, and the charge on each is positive.

 

[rude man]

x-component on q, and the charge on each is positive.

So if Q is restricted to the y axis, why wouldn't the answer be simply y=0?
The question would make more sense if it asked for the value of b to give the maximum y component on q.

 

[Physics2341313]

I don't understand? Q is restricted on the y-axis at a height of a = 3m the charge q is arbitrary at a location b. The first part of the problem is to find the value b at which the x-component of the force between the two charges is at it's miniumum which would be at b = 0. To find it's maximum the problem at hand now the derivative is involved for its maximum value? Which is what I was having trouble with. I am not seeing how the y-axis comes into the problem since Q is fixed at that location and the location of q on the x-axis is variant.

 

[rude man]

NM, I read the problem backwards.
Your post 1 is OK. Why not finish the problem?
the y-axis comes into the problem since the x force on q is dependent on the value of a. But a is constant so proceed with d/db (F_x) = 0 etc.

 

[Physics2341313]

Couldn't solve the derivative for b. I think I messed the derivative up I was getting high powers of b that couldn't be solved.

Sample of what I tried to solve...

d/db [b/(9+b^2)^{3/2}] \Rightarrow [3b(9 + b^2)^{1/2} - (9 + b^2)^{3/2}]/(9 + b^2)^3

After that it turned into a mess trying to solve for b

 

[Physics2341313]

Ahh, nevermind I solved it. I forgot that I could discard the denominator when setting equal to zero. Made the problem more complex than need be,

 

[rude man]

Couldn't solve the derivative for b. I think I messed the derivative up I was getting high powers of b that couldn't be solved.

Sample of what I tried to solve...

d/db [b/(9+b^2)^{3/2}] \Rightarrow [3b(9 + b^2)^{1/2} - (9 + b^2)^{3/2}]/(9 + b^2)^3

After that it turned into a mess trying to solve for b

First thing is you throw out the denominator (why can you do that?)
secod thing is you have the sign of the numerator wrong d(uv) = (v du - u dv)/v².
third thing is you didn't do the derivative right. One way to check is again using dimensions. Ignoring the denominator, your 1st term on the right has dimension L² while the second has L³ where L = length.
If you divide the numerator by a certain quantity the solution becomes very easy.
finally a small point: don't write "9", leave as a² until the end. Too many numbers mess up the math and make checking harder.
gotta go to bed (where are you located? in Hawaii or U.K.?

 

[rude man]

Ahh, nevermind I solved it. I forgot that I could discard the denominator when setting equal to zero. Made the problem more complex than need be,

OK. Good! Should still look at my post #11 for one or two points.