I Maximum Angle of Deflection for Colliding Particles

[neilparker62]

TL;DR

Trying to understand physics of maximum deflection

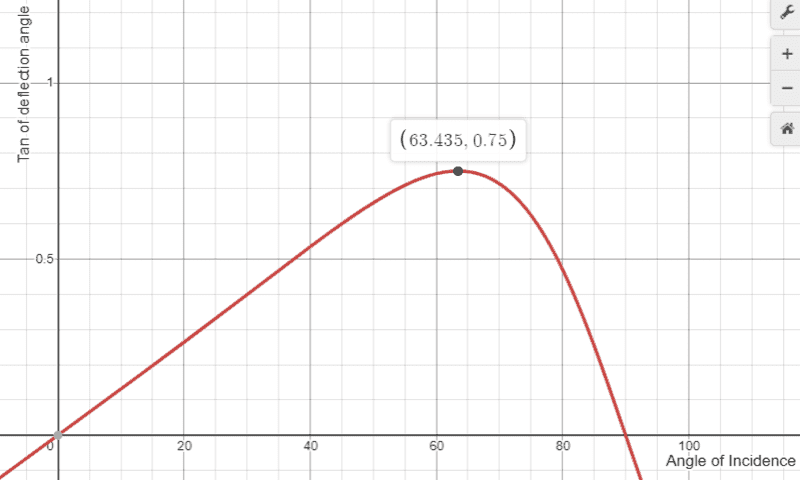
When a heavier mass (or nucleus say) collides with a lighter one, it deflects through a certain angle which has a theoretical maximum. There are numerous derivations for this maximum angle of deflection $(\sin\theta_{d_{max}}=m/M)$ where m is the small mass and M the larger but none seem to provide a clear physical explanation of what is going on. I tried to understand it in terms of energy transfer but got nowhere with that. So my question is what is physically going on when we reach maximum angle of deflection ? Is there something that physically defines when we move from a 'grazing' collision to a 'non grazing' collision ? Here for example is a plot of $\tan\theta_d$ vs $\theta_i$ where the latter angle of incidence is measured from the plane of contact. The mass ratio m/M in this case is 0.6 and so $\theta_{d_{max}}=36.87^{\circ}$ when $\theta_i=63.42^{\circ}.$

 

[gleem]

Below is a diagram that shows why the angle that the incoming body is scattered is always limited when its mass is greater than the target body's mass. The momenta of the two bodies are equal and opposite in the center of mass system but the velocities are not. The incoming mass dominates the velocity of the center of mass. Since the momentum of the incoming body in the center of mass system cannot be greater than 90° going to the lab system the center of mass velocity further increases its velocity reducing the scattering angle.

 

[neilparker62]

Thanks. I more or less understand why the angle of deflection is limited but I am trying to understand the exact physical conditions which are met when we reach the maximum angle.

 

[kuruman]

Thanks. I more or less understand why the angle of deflection is limited but I am trying to understand the exact physical conditions which are met when we reach the maximum angle.

Are you looking for some kind of rule like "when a projectile reaches maximum height its gravitational potential energy is maximum"?

 

[neilparker62]

Yes. Perhaps I'm missing something really obvious ?!