Maximum extension of a spring on an inclined plane

[Better WOrld]

Homework Statement

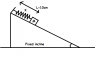
A block of mass $M = 1 kg$ is placed of a fixed rough incline of inclination

$\theta=sin^{-1} \frac{7}{10}$ and coefficient of friction $\mu=\frac{1}{\sqrt{51}}$. It is connected to a spring of spring constant 100 N/m. Initially the spring is in natural state with length = 10cm

If the block is left to move then find the final elongation in spring when block stops moving.

Take $g= 10m/s^2$

Homework Equations

The Attempt at a Solution

The forces doing work on the block are gravity, the spring force, and friction. Initially, the velocity of the block is 0 and once the spring reaches its maximum extension, the velocity again becomes 0, hence the change in Kinetic Energy of the bock is 0. Let the maximum extension of the spring be $X$.
\[\]
Applying the Work Energy Theorem,
$$W_{gravity}-W_{spring}-W_{friction}=\Delta K=0$$
$$mgX\sin\theta-\int_0^X kx dx-\mu mg\cos\theta X=0$$
$$mgX\sin(\sin^{-1}\dfrac{7}{10})-\dfrac{kX^2}{2}-\mu mg \cos(\sin^{-1}\dfrac{7}{10})=0$$
Putting in the given values,
$$7-50X-1=0$$
$$X=0.12m$$

However, this does not give the 'correct' answer - $0.8m$. I would be truly grateful if somebody could please explain where I have gone wrong. Thanks in advance!

 

[haruspex]

You have found the extension when the block first comes to a halt, but has it stopped moving entirely? Calculate the forces that will apply at that point.

 

[stockzahn]

$$mgX\sin\theta-\int_0^X kx dx-\mu mg\cos\theta X=0$$

You didn't take in account the oscillation of the system. Try to sum up all the forces at $X=0.12m$.

 

[Better WOrld]

You have found the extension when the block first comes to a halt, but has it stopped moving entirely? Calculate the forces that will apply at that point.

At that point, the spring would exert a force of $12N$ upwards while there is a force of $11N$ down the plane. However, I fail to see how that matters Sir.

 

[Better WOrld]

You didn't take in account the oscillation of the system. Try to sum up all the forces at $X=0.12m$.

Sir, please could you explain what you mean? Doesn't the velocity of the block become 0 at $0.12m$? If not, please could you show me how to solve the problem?

 

[stockzahn]

I think the task is to calculate the final position of the block. If you calculate the forces at $X=0.12m$ you will see that the block is going to be accelerated again.

 

[haruspex]

At that point, the spring would exert a force of $12N$ upwards while there is a force of $11N$ down the plane. However, I fail to see how that matters Sir.

The question is ambiguous. "Stops moving" could mean the first time the velocity is zero. That is how you have interpreted it. Or it could mean stops completely, i.e. comes to rest and stays at rest. If the forces are not in balance then it will start moving again.