Maximum tensile stress on rod with eccentric rotating tensile load

[biplab93]

I was solving this paper, but got stuck on this question, and it's been bugging me endlessly. I don't know what I'm missing. Here's the question:

A rod of 20 dia is fixed to the ceiling of a roof on one end. A rotor of 50 kg mass is attached to the free end with bearings. The CG of the rotor is 10 mm away from the shaft axis. The rotor is rotating at 600 rpm. The max tensile stress (in N/Sq.mm) in the rod is nearly equal to

A. pi/2
B. 200pi
C. 300pi
D. 400pi (correct answer)

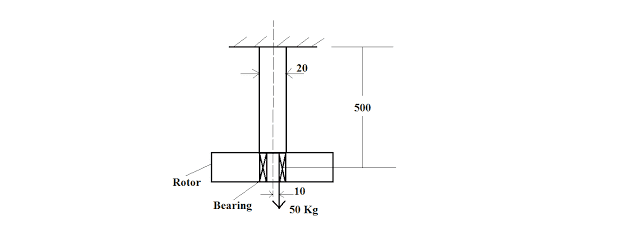
Because of the bearings, there will be no torsional load on the rod (right?). That only leaves out the eccentric tensile load. So I converted that into an axial tensile load and a bending moment (50g*10 Nmm), and the resulting bending stress is: 1.6 (axial) + 6.3 (bending) N/mm^2 = 7.9. (Bending stress = M*y/I. y=max distance from neutral axis)

That's a far cry from 400pi. I don't know how the length of the rod (500mm) or the speed of the rotor (600rpm) will be incorporated, or if they will be needed at all.

Help will be much appreciated. Thanks in advance.

 

[AlephZero]

Because of the bearings, there will be no torsional load on the rod (right?).

Right.

That only leaves out the eccentric tensile load.

No ...

I don't know how the length of the rod (500mm) or the speed of the rotor (600rpm) will be incorporated, or if they will be needed at all.

The CG of the rotor is moving in a circle radius 10mm at 600 RPM. What force is acting on the rotor to make it do that? How is that force transmitted through the rod?

 

[Sia]

I was able to get the answer, however, I am not totally convinced. It's like:

We know tensile stress would be σ= 32 M / Πd^3

Now bending moment M will be due to the eccentric loading as well as due to the centrifugal force acting on the rod as a result of rotor's CG rotation.

So, M= m.g.e + m. ω^2. e.L
=(50 X 10 X 10 ) + {50 X(600X2Π/60)^2 X10X 0.500}
=5000 + 100000Π^2
As 100000Π^2>> 5000,
5000 seems to be ignored (for simplifying calculation)

∴ σ=32X 100000Π^2/(Πx20^3)
=400Π