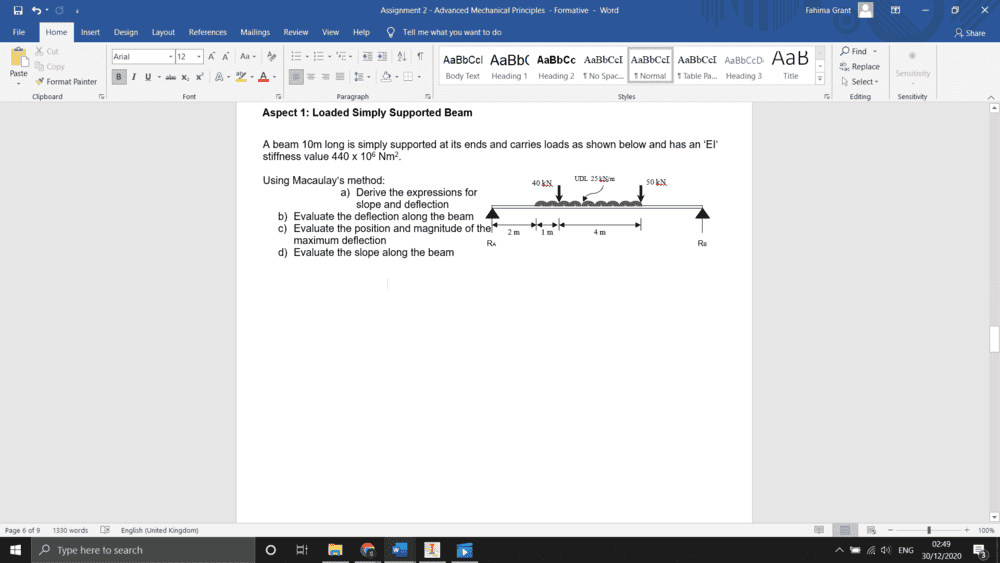
The discussion focuses on solving McCauley's Beam Problem, specifically addressing the need for correct expressions for deflection and displacement. The correct bending moment equation is identified as M_{x-x}=1032.5-215x, which incorporates the distributed load. Participants emphasize the importance of including all variables in calculations, such as the length of the distributed load and the products of the terms involved. The conversation highlights the necessity of understanding maximum deflection (ymax) and its relation to displacement.
PREREQUISITESEngineering students, structural analysts, and professionals involved in beam design and analysis will benefit from this discussion, particularly those seeking to deepen their understanding of deflection and bending moment calculations.