Mean and Gaussian curvature for a Gaussian 'hill' seem wrong

[Zaent]

I'm hoping someone can help check whether my final contour plots look plausible based on the surface.

I haven't done too much differential geometry but I've needed to work with Gaussian/Mean curvature for a simple 3D gaussian surface. Here's an example:

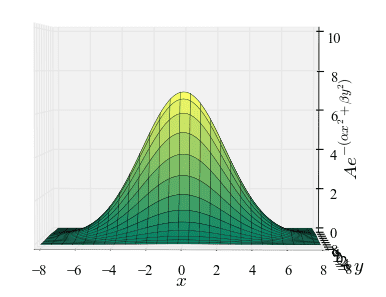
(A = 7, a=b=1/(3.5)^2)

It's parameterised using Monge patch representation; the z axis is f(x,y) = Ae^-(ax^2+by^2).

The Gaussian curvature K and Mean curvature H can be approximated via the following:

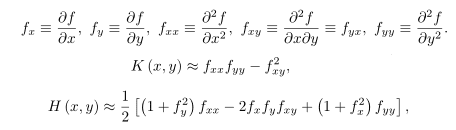
A little bit of calculation later, I end up with:

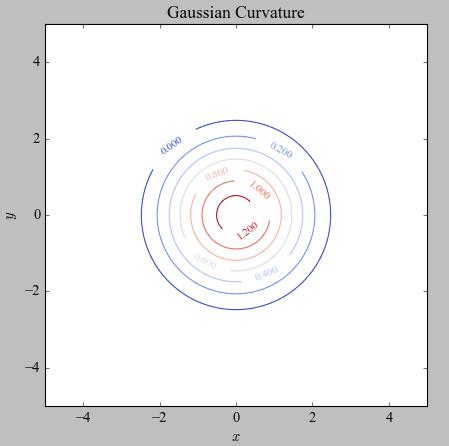
and

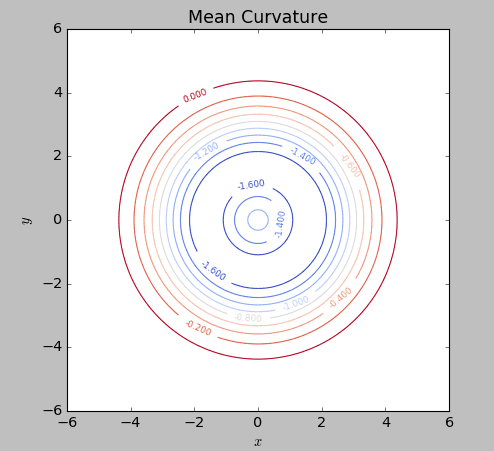These don't look right to me, considering on my example surface there's clearly curvature beyond x=y~4 range. Also, should the Gaussian and Mean contours look more similar? If it seems like my method is sound yet these still look wrong then the error must be in my calculation code. I haven't been able to spot a mistake in it, though.

Many thanks.

 

[andrewkirk]

I get K(0,5)=-0.07, so it looks to me like the calculations behind the contour graph of Gaussian Curvature are wrong.

Also, it looks from the first contour graph as though you are getting positive curvatures. They should be negative, as one can see from the shape of the 3D graph.

What formulas did you get for $f_{xx},\ f_{yy},\ f_{xy}$?

 

[Zaent]

I get K(0,5)=-0.07, so it looks to me like the calculations behind the contour graph of Gaussian Curvature are wrong.

Also, it looks from the first contour graph as though you are getting positive curvatures. They should be negative, as one can see from the shape of the 3D graph.

What formulas did you get for $f_{xx},\ f_{yy},\ f_{xy}$?

Thank you for taking the time.

Here's what I have for the Gaussian curvature and how I got it:

My method for Mean curvature is similar.

Should all the Gaussian curvatures be negative? I had in my head that it'd be negative at the bottom and positive at the top, based on a few other surfaces I googled for comparison.

 

[andrewkirk]

Thank you for taking the time.

Here's what I have for the Gaussian curvature and how I got it:

Your formula for K matches mine. Check the calculations you did with that formula. The values I get for y=0, x=(-6):6 are

-0.01784834 -0.06794136 -0.15450102 -0.14104856 0.23583912 0.92825319 1.30612245
0.92825319 0.23583912 -0.14104856 -0.15450102 -0.06794136 -0.01784834

These are different from the numbers on the contour graph.

Should all the Gaussian curvatures be negative? I had in my head that it'd be negative at the bottom and positive at the top, based on a few other surfaces I googled for comparison.

What you had in your head is right, and is what I meant. It does not match the contour graph, which seems to show only positive values.

 

[Zaent]

Your formula for K matches mine. Check the calculations you did with that formula. The values I get for y=0, x=(-6):6 are

-0.01784834 -0.06794136 -0.15450102 -0.14104856 0.23583912 0.92825319 1.30612245
0.92825319 0.23583912 -0.14104856 -0.15450102 -0.06794136 -0.01784834

These are different from the numbers on the contour graph.
What you had in your head is right, and is what I meant. It does not match the contour graph, which seems to show only positive values.

I did this and got the exact same values, so then I checked my contour and changed how many lines it was showing. Duh. Here's what I have now:

I figure this must be right and I just wasn't showing enough lines. One thing that worries me is the mean curvature, should those all be negative? Here's the formula I get for that:

Thank you again, you're a saint.

 

[andrewkirk]

One thing that worries me is the mean curvature, should those all be negative?

The formula is a little too busy to check. I suggest you factorise it, to get all the common factors out of the way - the exponent and the constant A for a start. Also, it's better to write short formulas for $f_x,f_{xx},f_{xy}$ etc and then write the formula for $H$ in terms of those, to prevent the formula getting too big. Then you can check it for correctness.

FWIW I got the following values for H for y=0 and x= -6:6

0.09410179 0.05881300 -0.03535662 -0.12436133 -0.23370455 -0.50643935 -1.14285714
-0.50643935 -0.23370455 -0.12436133 -0.03535662 0.05881300 0.09410179

Omitting the denominator, which your formula above does, gives:

0.1132960 0.1136231 -0.1425589 -0.8866893 -1.6761835 -1.5515235 -1.1428571
-1.5515235 -1.6761835 -0.8866893 -0.1425589 0.1136231 0.1132960

The signs change, from + to - and back to +.

 

[Zaent]

The formula is a little too busy to check. I suggest you factorise it, to get all the common factors out of the way - the exponent and the constant A for a start. Also, it's better to write short formulas for $f_x,f_{xx},f_{xy}$ etc and then write the formula for $H$ in terms of those, to prevent the formula getting too big. Then you can check it for correctness.

FWIW I got the following values for H for y=0 and x= -6:6

0.09410179 0.05881300 -0.03535662 -0.12436133 -0.23370455 -0.50643935 -1.14285714
-0.50643935 -0.23370455 -0.12436133 -0.03535662 0.05881300 0.09410179

Omitting the denominator, which your formula above does, gives:

0.1132960 0.1136231 -0.1425589 -0.8866893 -1.6761835 -1.5515235 -1.1428571
-1.5515235 -1.6761835 -0.8866893 -0.1425589 0.1136231 0.1132960

The signs change, from + to - and back to +.

I have the same values. Number of contour lines was the problem again. I appreciate all the help!