Discussion Overview
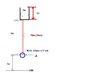
The discussion revolves around measuring the pressure of water in a tank situated on a rooftop, specifically at a height of 1 meter from the ground. Participants explore various methods and calculations related to pressure measurement, considering factors such as the height of the water column and the diameter of the hose used for water discharge.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant seeks advice on measuring the pressure at 1 meter height from the ground, given the dimensions of the water tank and the hose diameter.
- Another participant explains that pressure can be calculated using the formula for weight divided by area, suggesting that the pressure at the end of the hose can be derived from the density of water and the height of the water column.
- Concerns are raised about the losses due to the hose affecting the final pressure, with a suggestion that a gauge might be the best way to measure it.
- Participants discuss the calculations for pressure at a specific point, with one providing detailed steps involving the volume of water and its weight, leading to a calculated pressure value.
- There is a mention of discrepancies in pressure calculations, with one participant noting that the pressure calculated exceeds typical values expected from a 4-meter water column.
- Another participant emphasizes that only the water column directly above the measurement point contributes to the pressure, referencing Pascal's law.
- One participant shares information about their pressure measuring sensor's range and expresses intent to implement a project based on the discussion.
Areas of Agreement / Disagreement
Participants express differing views on the calculations for pressure at point A, with some calculations suggesting excessively high pressures while others align with expected values based on fluid mechanics principles. The discussion remains unresolved regarding the exact pressure measurement and the factors influencing it.
Contextual Notes
There are unresolved assumptions regarding the impact of the hose on pressure measurements, and participants have not reached a consensus on the correct approach to calculating the pressure at the specified height.