- #1
PA3040
- 10
- 0
Dear All
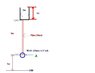
My water tank fixed on roof top 5M from the ground
Height of tank 1m
width of tank .75m ( Cylinder type water tank )
if water out from the tank by .5 inch hose
how can I measure the pressure at 1m height from the ground
Please advice
Thanks in advance
My water tank fixed on roof top 5M from the ground
Height of tank 1m
width of tank .75m ( Cylinder type water tank )
if water out from the tank by .5 inch hose
how can I measure the pressure at 1m height from the ground
Please advice
Thanks in advance
Last edited: