SUMMARY
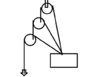
The discussion centers on the mechanical advantage of a pulley system, specifically addressing the tension in ropes connected to multiple pulleys. It is established that in an ideal scenario with massless pulleys, the tension (T) in the ropes remains equal on both sides of each pulley. However, the complexity arises when considering the forces acting on the middle pulley, which requires a free body diagram and an understanding of the angles of the ropes. The conclusion is that without knowing these angles, the problem cannot be accurately solved.
PREREQUISITES
- Understanding of basic physics concepts related to forces and tension
- Familiarity with free body diagrams
- Knowledge of pulley systems and mechanical advantage
- Basic trigonometry for analyzing angles in pulley systems
NEXT STEPS
- Study the principles of mechanical advantage in pulley systems
- Learn how to create and analyze free body diagrams
- Explore the effects of angle variations on tension in ropes
- Investigate real-world applications of pulley systems in engineering
USEFUL FOR
Physics students, mechanical engineers, and anyone interested in understanding the dynamics of pulley systems and mechanical advantage.