Mechstudent
- 2
- 0
1. In my materials science's exam, I had the following question: What would be the maximum force F to cause failure in a block that has been drilled at two place?
See following drawing:
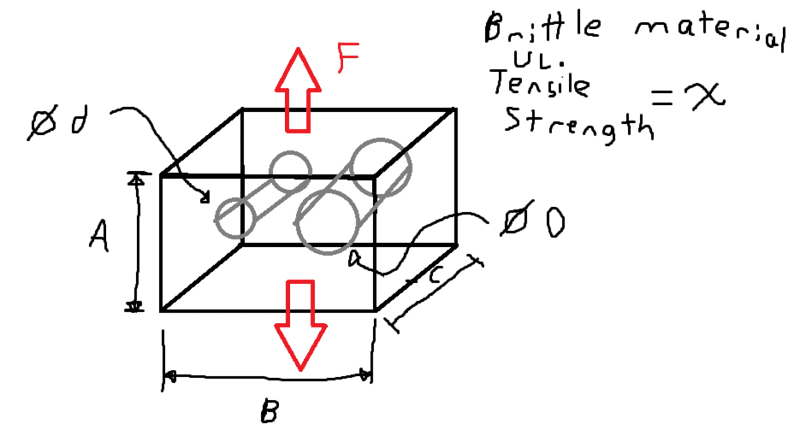
(Lame paint skills, I know..)
2. Homework Equations
1) D/W
2) σ = F/S
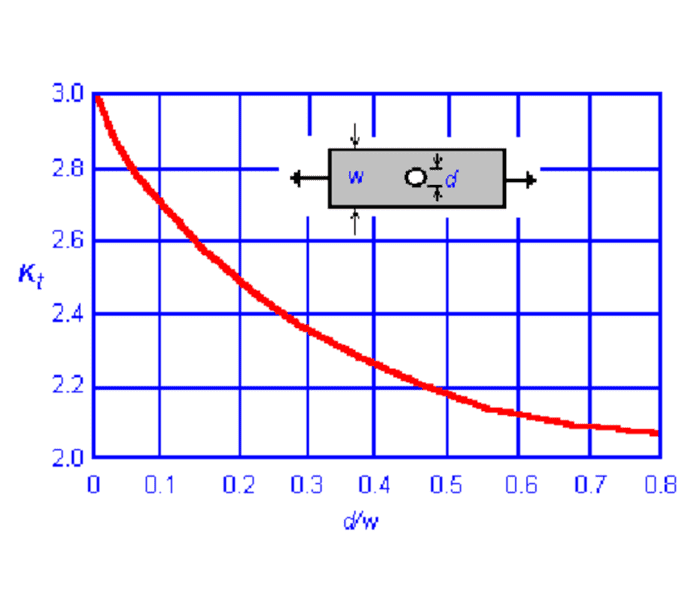
1)First, I calculated both D/W ratios. In this case, D/B and d/B
2)Once I had this ratio, I found the corresponding K factors by using the Stress Concentration Chart for hole in a plate.
3) This is where I get blocked. I am unsure what to do with the factors. What I did was pick the hole with the highest corresponding K factor, and ignore the other. I do not know if I have to interpolate between or add them somehow.
4) Using σ = F/S, I know that σ*S = F and that:
S = C * (B-d-D) which is the area of the top rectangle
Since the material is brittle, The ultimate strength is the maximum
So:
x * C * (B-d-D) = F
Because there is stress concentration, The result has to be divided by the factor K.
So my answer was
(x * C * (B-d-D))/K = F max
I wasn't able to find an example where there is more than a single stress concentration area(in this case, two holes instead of one), So I do not know how it adds up, and whether all the necessary information is in the image or not.
See following drawing:
(Lame paint skills, I know..)
2. Homework Equations
1) D/W
2) σ = F/S
The Attempt at a Solution
1)First, I calculated both D/W ratios. In this case, D/B and d/B
2)Once I had this ratio, I found the corresponding K factors by using the Stress Concentration Chart for hole in a plate.
3) This is where I get blocked. I am unsure what to do with the factors. What I did was pick the hole with the highest corresponding K factor, and ignore the other. I do not know if I have to interpolate between or add them somehow.
4) Using σ = F/S, I know that σ*S = F and that:
S = C * (B-d-D) which is the area of the top rectangle
Since the material is brittle, The ultimate strength is the maximum
So:
x * C * (B-d-D) = F
Because there is stress concentration, The result has to be divided by the factor K.
So my answer was
(x * C * (B-d-D))/K = F max
I wasn't able to find an example where there is more than a single stress concentration area(in this case, two holes instead of one), So I do not know how it adds up, and whether all the necessary information is in the image or not.