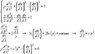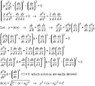- #1
LAHLH
- 409
- 1
Hi,
could anyone tell me what methods I would need to solve this system:
[tex] y\frac{d^2 y}{d\lambda^2}+\left(\frac{dx}{d\lambda}\right)^2-\left(\frac{dy}{d\lambda}\right)^2=0 [/tex]
[tex] \frac{y}{2}\frac{d^2x}{d \lambda ^2}-\left(\frac{dx}{d\lambda}\right)\left(\frac{dy}{d\lambda}\right)=0 [/tex]
I believe the solution is [tex] (x-x_0)^2+y^2=l^2 [/tex]
I think (unless I've made a mistake anyway) that these are the geodesic equations for H^2, so the solutions are semicircles in the upper half plane (cf Sean Carroll). I'm not sure how to solve these however despite him saying "it is straightforward to show...", because they seem to be non linear and second order.
Thanks
could anyone tell me what methods I would need to solve this system:
[tex] y\frac{d^2 y}{d\lambda^2}+\left(\frac{dx}{d\lambda}\right)^2-\left(\frac{dy}{d\lambda}\right)^2=0 [/tex]
[tex] \frac{y}{2}\frac{d^2x}{d \lambda ^2}-\left(\frac{dx}{d\lambda}\right)\left(\frac{dy}{d\lambda}\right)=0 [/tex]
I believe the solution is [tex] (x-x_0)^2+y^2=l^2 [/tex]
I think (unless I've made a mistake anyway) that these are the geodesic equations for H^2, so the solutions are semicircles in the upper half plane (cf Sean Carroll). I'm not sure how to solve these however despite him saying "it is straightforward to show...", because they seem to be non linear and second order.
Thanks