rushikesh
- 20
- 1
The M-M expt. concluded the constancy of speed of light, by emitting a beam of light, one horizontally and other vertically to the direction of the motion of the earth. Since they returned from the mirror to the source at the same time (having no effect of Earth's motion on them) it was concluded that light speed is constant and independent of the source.
The problem:
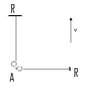
My argument is, even if we replace the beam of light by two ordinary balls, the result is the same, i.e. they will return to the source at the same time (considering equal distance traveled and common speed). To explain in detail (refer to attachment):
If the two balls start at pt. A, one horizontally and second perpendicular to other and if they return from two reflectors R equidistant from A, they reach the source A, at the same time. This is true even if this set up is on a uniform moving train as shown.
Here we won't conclude that the speed of the balls is constant irrespective of the motion, as we have concluded for light. Kindly explain.
The problem:
My argument is, even if we replace the beam of light by two ordinary balls, the result is the same, i.e. they will return to the source at the same time (considering equal distance traveled and common speed). To explain in detail (refer to attachment):
If the two balls start at pt. A, one horizontally and second perpendicular to other and if they return from two reflectors R equidistant from A, they reach the source A, at the same time. This is true even if this set up is on a uniform moving train as shown.
Here we won't conclude that the speed of the balls is constant irrespective of the motion, as we have concluded for light. Kindly explain.