Michelson Interferometer ring contraction

[epsilon]

I have been trying for hours to understand what is physically causing the interferometric rings to contract when the separation of the mirrors is reduced.

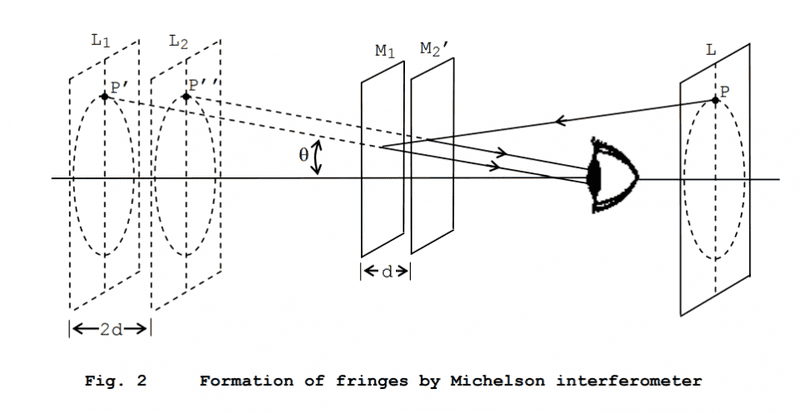
From the equation: m\lambda = 2Lcos\theta, where m is the number of fringes, if we consider just one fringe at a fixed wavelength, m\lambda is constant and hence 2Lcos\theta is also constant.

Hence reducing L causes cos\theta to increase, which is analogous to reducing \theta. [Is this where I'm going wrong?]

Question 1: When reducing d in the image above, does it matter if we are moving L_1 towards L_2 or vice versa? (Is it directionally dependent?)

Question 2: The image suggests that \theta is only linked to L_1. If I move L_1 towards L_2, the adjacent side of the right-angled triangle is getting shorter, and hence \theta must be increasing. But this goes against what happens when it is considered mathematically.

How can we tell PHYSICALLY whether the rings are contracting or expanding? Thank you.

 

[blue_leaf77]

Hence reducing L causes cos\theta to increase, which is analogous to reducing \theta. [Is this where I'm going wrong?]

That's correct, and should confirm that the fringes contract when the mirror separation is reduced.

Question 1: When reducing d in the image above, does it matter if we are moving L1L_1 towards L2L_2 or vice versa? (Is it directionally dependent?)

It doesn't matter.

Question 2: The image suggests that θ\theta is only linked to L1L_1. If I move L1L_1 towards L2L_2, the adjacent side of the right-angled triangle is getting shorter, and hence θ\theta must be increasing. But this goes against what happens when it is considered mathematically.

I don't get your point.

How can we tell PHYSICALLY whether the rings are contracting or expanding? Thank you.

I think you can place a movable marker on a particular fringe, when you decrease $d$, this marker should go radially inward. That's when you would say the fringes are contracting.
Btw, notice that the zeroth order is located at infinity. This means, if you decrease $d$, all fringes will actually contract such that in the end there is only bright area on the screen when $d=0$, i.e. when the mirrors coincide.

 

[epsilon]

That's correct, and should confirm that the fringes contract when the mirror separation is reduced.

It doesn't matter.

I don't get your point.

I think you can place a movable marker on a particular fringe, when you decrease $d$, this marker should go radially inward. That's when you would say the fringes are contracting.
Btw, notice that the zeroth order is located at infinity. This means, if you decrease $d$, all fringes will actually contract such that in the end there is only bright area on the screen when $d=0$, i.e. when the mirrors coincide.

Thank you, that was quite helpful (still slight uncertainty but better understanding now than before!)