Miller indices of a plane in a simple cube

[ksac]

I am trying to get a hang of miller indices and doing some practice.

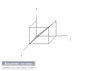
So here it is : What would be the miller indices of the plane containing the x-axis and equally inclined to y and z axes?

(I have uploaded the diagram and highlighted the plane to clarify)

Attempts :

I first try to find the intercepts.
The intercepts on the y and z axes are both, 0.
So does that make the corresponding miller indices k and l infinity? If yes, isn't the whole point of miller indices to avoid infinities in case of planes parallel to any of the crystal axes?

Also, what would be the intercept on the x axis, since the plane contains the x axis?

If there any gaps in my understanding or flaws in the way i am looking at it, please do correct me.
thank you :)

 

[nickjer]

I believe this might be the wrong section since this isn't Introductory Physics. Also, you need to know where the plane intersects the three cubic lattice vectors. Since you have the whole plane intersecting the x-axis, you can use the periodicity of the crystal lattice to either move the plane by one lattice vector, or move your origin one lattice vector in the y-direction.

By doing that, you can see now that the plane never intersects the x-axis, and that it intersects y=-1 and z=+1. After taking the inverses, you are left with (h,k,l) = (0,-1,1).

 

[ksac]

yes that makes a lot of sense. thank you :)