Min max problem: length of pipe from 2 towns to the river

[Karol]

Homework Statement

Homework Equations

Minimum/Maximum occurs when the first derivative=0

The Attempt at a Solution

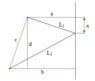
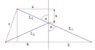
$$l_1^2+l_2^2=(a^2+x^2)+[b^2+(d-x)^2]=a^2+b^2+x^2+\left[ \sqrt{c^2-(b-a)^2}-x \right]^2$$
$$(l_1^2+l_2^2)'=2x+2\left[ \sqrt{c^2-(b-a)^2}-x \right](-1)$$
$$(l_1^2+l_2^2)'=0~~\rightarrow~~x=\frac{1}{2}\sqrt{c^2-(b-a)^2}=\frac{d}{2}$$
The minimum (or maximum?) distance is when the station is in the middle of the vertical distance between the cities
The total pipe's distance is:
$$Dist=\sqrt{l_1}+\sqrt{l_2}=\sqrt{a^2+x^2}+\sqrt{b^2+x^2}=\sqrt{a^2+\frac{d^2}{4}}+\sqrt{b^2+\frac{d^2}{4}}$$
It doesn't give $~\sqrt{c^2-4ab}$

 

[Orodruin]

You are supposed to minimise the sum of the lengths (i.e., $L_1 + L_2$) not the sum of the squares of the lengths ($L_1^2 + L_2^2$).

 

[verty]

Hint: Imagine b is on the other side but d is still the same.

 

[Karol]

You are supposed to minimise the sum of the lengths (i.e., $L_1 + L_2$) not the sum of the squares of the lengths ($L_1^2 + L_2^2$).

But if the square of the lenghts is minimum then the length is also minimum
I will think about the hint that b is on the other side

 

[Orodruin]

But if the square of the lenghts is minimum then the length is also minimum

No, this is not true. It is true for a single length, not for the sum of lengths.

 

[Orodruin]

To expand a bit on that. Note that
$$
(L^2)' = 2LL'
$$
so, for a single length, $L' = 0$ if $(L^2)' = 0$. However, you have the sum of two lengths and
$$
((L_1+L_2)^2)' = 2(L_1+L_2) (L_1+L_2)' = [L_1^2 + L_2^2 + 2L_1 L_2]' = (L_1^2 + L_2^2)' + 2(L_1 L_2' + L_1' L_2).
$$
Note that $(L_1^2 + L_2^2)' = 0$ no longer guarantees that $(L_1 + L_2)' = 0$ as there are additional terms on the right-hand side.

 

[Karol]

Hint: Imagine b is on the other side but d is still the same.

$$\frac{a}{x}=\frac{b}{\sqrt{c^2-(b-a)^2}-x}~\rightarrow~x=\frac{a\sqrt{c^2-(b-a)^2}}{a+b}$$
$$l_1+l_2=...=\sqrt{c^2+4ab}$$

 

[verty]

View attachment 229938
$$\frac{a}{x}=\frac{b}{\sqrt{c^2-(b-a)^2}-x}~\rightarrow~x=\frac{a\sqrt{c^2-(b-a)^2}}{a+b}$$
$$l_1+l_2=...=\sqrt{c^2+4ab}$$

You are given a,b,c. Your first task is to find d. Then find L1+L2 when it is the shortest configuration.

 

[Orodruin]

You are given a,b,c. Your first task is to find d. Then find L1+L2 when it is the shortest configuration.

I think the $\ldots = \sqrt{c^2 + 4ab}$ means he solved it ...