- #1
Karol
- 1,380
- 22
Homework Statement
Homework Equations
Minimum/Maximum occurs when the first derivative=0
GM≤AM: ##~\sqrt{xy}\leq\frac{x+y}{2}##
The Attempt at a Solution
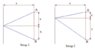
If the sum of squares of the distances (setup 2) in an arbitrary point is bigger than the sum of the squares of the shortest distances (setup 1, the mid point between A and B) then the distance from an arbitrary point is also bigger. i want to prove without calculus that:
$$2s^2+x^2+y^2\geq 2s^2+2\left[ \frac{x+y}{2} \right]~\rightarrow~\frac{3}{2}(x^2+y^2)\geq xy$$
I want to use GM≤AM so i take the square root of what i need to prove, and i need to prove:
$$\sqrt{1.5}\sqrt{x^2+y^2}\geq\sqrt{xy}$$
I know ##~\sqrt{xy}\leq\frac{x+y}{2}~## so i have to prove:
$$\sqrt{xy}\leq\frac{x+y}{2}\leq\sqrt{1.5}\sqrt{x^2+y^2}$$
And it remains that i have to prove:
$$\frac{x+y}{2}\leq\sqrt{1.5}\sqrt{x^2+y^2}$$
I know ##~\sqrt{(x+y)^2}=\sqrt{x^2+y^2+2xy}\leq\sqrt{x^2+y^2}~## but it doesn't help since i need to insert an inequality
on the left of ##~\sqrt{1.5}\sqrt{x^2+y^2}~## and not on the right side.