blue_eyes_88
- 7
- 1
- Homework Statement
- What is the smallest height for a projectile to hit the target?
- Relevant Equations
- Kinematic equations
A plane is flying 80km/h in horizontal direction and it has to drop a bomb into 30m wide and 30m deep hollow. What is the smallest possible height for the plane to fly above hollow if the bomb successfully hits the bottom?
I made a mistake somewhere but not sure where... the correct result is 335m
My solving so far:
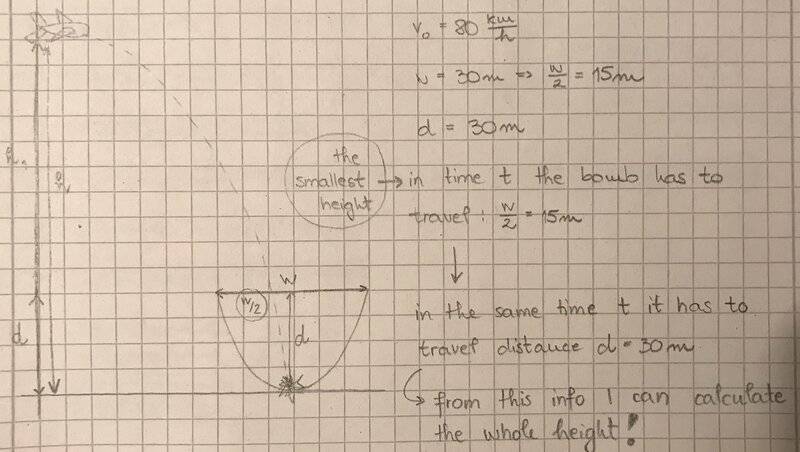

I made a mistake somewhere but not sure where... the correct result is 335m
My solving so far: