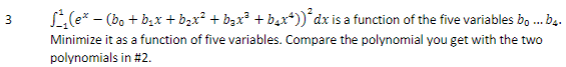- #1
Lady M
- 9
- 0
- Homework Statement
- I am given an integral with the bound of -1 to 1, of e^x minus a string of polynomials , x^n, running from 0 to 4, all times constants b[n], running from 0 to 4, all of which is squared. (sorry I don't know how to type functions into this interface yet, but I will include a photo of the question below).
I am asked to "minimize it as a function of 5 variables". Then it wants me to compare the polynomial I get to the Taylor series of e^x to 4 terms, as well as another series approximation of e^x obtained earlier using the inner product of Legendre polynomials.
- Relevant Equations
- The problem is that I am not sure what's being asked here. Specifically, I am not sure what "minimize the function" means in this context.
I found this post here (https://www.physicsforums.com/threads/minimizing-a-integral.533829/) from a while back, which seems to be addressing a similar question. However, it looks like the "resolution" to the question came from using shifted Legendre polynomials, and then using that to determine the coefficients. Because my class has not done something like that yet, I doubt that's what she wanted us to do.
As promised, here is the original question, with the integral written in a more legible form.