- #1
LCSphysicist
- 645
- 161
- Homework Statement
- I am trying to orthogonalize {1,x,x²}
- Relevant Equations
- Just the inner product of functions space.
Suppose p = a + bx + cx².
I am trying to orthogonalize the basis {1,x,x²}
I finished finding {1,x,x²-(1/3)}, but this seems different from the second legendre polynomial.
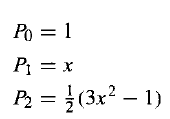
What is the problem here? I thought could be the a problem about orthonormalization, but check and is not.
I am trying to orthogonalize the basis {1,x,x²}
I finished finding {1,x,x²-(1/3)}, but this seems different from the second legendre polynomial.
What is the problem here? I thought could be the a problem about orthonormalization, but check and is not.