Minimizing the friction of the end of a lever against the top of a moving piston

[Anachronist]

TL;DR Summary

Trying to figure out an approach to calculate points on a curve on the underside of a lever to minimize friction as the lever and piston move together, maintaining contact.

I'm trying to design a simple mechanism in CAD and got stuck on this problem.

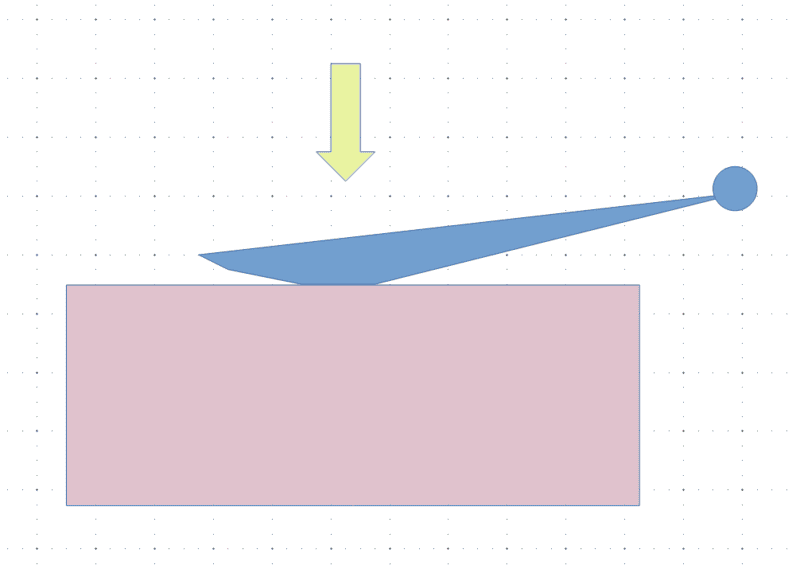
Consider a lever (blue shape) that pivots at one end (blue circle). The other end rests on a piston (pink rectangle). In my application the lever is pushing the piston (the lever pushes through the full travel of a button under one end), but it's the same problem if the piston moves the lever.

If the lever is a thin straight line, the end of the lever would rub against the top of the piston as the piston moves up or down. These parts are going to be unlubricated plastic, and rubbing might result in some wear after a few thousand cycles.

I'm trying to figure out an approach to calculate points along a curve on the underside of the lever to approximate rolling friction, to minimize the rubbing as the lever and piston move through a small range of motion. At the top of the piston's range, the lever would start horizontal or nearly so, and the lever's angular range of motion is at most 25°.

As the piston moves down, the lever would need to lengthen to maintain the same point of contact, which implies some sort of curved surface, as shown in the drawing above. I know it can't maintain the same contact point and have rolling friction, so the curve should lengthen the lever and allow the lever's underside surface to roll across the piston surface.

The more I think about it, the more it seems like I need to calculate this numerically. That isn't a problem (I do such calculations in the CAD software for other purposes), I just don't know how I would set up this particular problem. This seems like such a common application, it must have been dealt with before, but I don't know what to search for information that would help.

 

[jrmichler]

Two scenarios:
1) The lever is curved such that it contacts the center of the piston over its full range of travel. In that case, the piston is always loaded in the center, while the lever must slide against the top of the piston.

2) The lever is curved such that it rolls across the top of the piston. In that case, the piston is loaded off center over all but one position of the lever. Off center loading puts loads on the sides of the piston. The magnitude of those loads depend on the length of the piston.

Either way, something is sliding under load. Modern plastics can last a lot longer than a few thousand cycles under sliding loads, depending on the sliding load, sliding speed, sliding contact pressure, ambient temperature, and environmental conditions such as dirt and moisture.

I do not have a solution for the curve to get rolling action off the top of my head, but your problem seems to be similar to that of an involute tooth gear rolling against a rack. The teeth of the gear are curved, while the teeth of the rack have straight sides. The gear teeth have a profile designed to minimize sliding action, but there is always some sliding action. The sliding can be minimized by proper gear tooth design, but cannot be eliminated.

I think that your case is very similar. If so, you can minimize, but not eliminate sliding. If you decide to live with sliding, give us more information on the application, and we can help you select an appropriate plastic.

 

[Tom.G]

Try this easy experiment for another approach:

1) hold your arm and hand horizontal in front of you
2) make a fist
3) partially extend first finger so the tip points down
4) flex your wrist up and down

Without doing the math, it may be advantageous if the pivot elevation is located half way between the piston travel limits.

Cheers,
Tom

 

[Anachronist]

Two scenarios:
1) The lever is curved such that it contacts the center of the piston over its full range of travel. In that case, the piston is always loaded in the center, while the lever must slide against the top of the piston.

2) The lever is curved such that it rolls across the top of the piston. In that case, the piston is loaded off center over all but one position of the lever. Off center loading puts loads on the sides of the piston. The magnitude of those loads depend on the length of the piston.

This will be a 3D printed part, likely using PETG or PLA, neither of which wear as well as ABS, which is likely what the button/piston is made from (it's a keyboard switch, designed for imperfectly centered loads). The application is a lever that repeatedly pushes the button.

I'd be happy with either scenario. The button switch in question has a fairly long length, much longer than the size of the surface the lever would slide on. The contact area between the lever and the top of the button/piston is quite small so I was concerned about extra wear at that point. I would prefer scenario 2, but failing that, scenario 1 would work. I may end up just putting an arbitrary curve on the lever that "looks" right at both extremes of the movement with the touch points starting and ending a little wa off either side of the center, and be done with it.

Good analogy with gear teeth. The only kind of gear teeth I know of that are supposed to have only rolling friction are those cut using a rack with cycloidal teeth. A while back I attempted to make one for 3D printing:

 

[Anachronist]

Try this easy experiment for another approach:

1) hold your arm and hand horizontal in front of you
2) make a fist
3) partially extend first finger so the tip points down
4) flex your wrist up and down

Without doing the math, it may be advantageous if the pivot elevation is located half way between the piston travel limits.

Great minds think alike! I did a similar experiment using pieces of cutout paper and a pin for a pivot.

Intuitively, I thought the same thing about the location of the pivot. As I thought about it more, it seemed like the best location would be at the top. Lower down would cause a curved surface to slide more rather than roll.

 

[Baluncore]

... but your problem seems to be similar to that of an involute tooth gear rolling against a rack. The teeth of the gear are curved, while the teeth of the rack have straight sides.

That is the key to the solution.

Good analogy with gear teeth. The only kind of gear teeth I know of that are supposed to have only rolling friction are those cut using a rack with cycloidal teeth.

Unlike the simulation you show, the shape of an involute gear tooth, depends on the diameter of the gear. The rack has a flat face, as does the hob that is used to generate a circular gear wheel in a hobbing machine.

 

[jack action]

Note that with the rack and pinion example in post #2, the top of your piston just needs to be slanted and the solution applies directly to your case.

 

[Anachronist]

@jrmichler @Baluncore Thank you. The gear-cutting concept worked. Instead of deriving a formula for a curve, all I had to do is use my CAD software to cut the top of the piston out of the pad on the end of the lever at several orientations in which they would come into contact. I used the center of the piston and lever pad as the center of the "gear teeth" height, and rotated the lever while the piston moved, making cuts into the pad along the way. The result is a nice smooth curve, for the case of the lever pivot being level with the piston at the top of its travel (pivot is way off past the right of this image):

As this pad pushes down on the top of the piston, it rotates counterclockwise and should rub minimally.

If I allow the piston to rise above the lever's pivot, then the other side of the pad gets cut, leaving a sharp point a little to the left of where the curve leaves the X axis.

 

[Juanda]

It seems I'm late to the party and you already found a simple solution that works well for what you need.
Still, I just wanted to add that, since your lever is 3D printed you can make the geometries as complex as you like without too much added cost. You could make a lever with a loose wheel at the end so the contact between the piston and the wheel is really rolling instead of an approximation as you initially mentioned in the OP.

For example, it could be possible to make a print-in-place lever + wheel on a shaft with clearance so rolling works without much resistance. Or maybe a snap-on print. Assemblies with screws could work too and the screw could be the shaft. In any case, the dynamic friction would happen at the shaft assuming you are not using bearings but you can make the shaft strong enough to make sure it'll outlast your application or print a new one (same or redesigned) when it breaks.

That kind of geometry would change the point of contact at the piston depending on the angle of the lever as you are aware but you didn't mention that as a problem. Also, that change in position would depend on the rotation axle for the lever so you can probably minimize it if necessary.

Anyways, I feel what you have so far already works just fine but I would not be able to take the thread out of my head if I didn't post this after it came to me.

 

[Lnewqban]

This seems like such a common application, it must have been dealt with before, but I don't know what to search for information that would help.

Please, see:
http://507movements.com/mm_337.html

 

[Juanda]

Please, see:
http://507movements.com/mm_337.html

I was curious about the mechanism and something didn't fit in my head so I plotted it. It isn't really pure vertical motion, right? Still, it is possible to make it very close to it for a given small angular displacement if the lateral arms are long enough and the circles they describe cross each other so the little misalignments will be absorbed by the clearance of the linkages.

I wonder if there is a possible configuration of that the middle point of that 4 arms mechanism really stays in a vertical line. I can't find the solution now using simple drawings but I feel there should be an easy mathematical proof for it.

 

[Lnewqban]

https://en.wikipedia.org/wiki/Straight-line_mechanism#Perfect_straight_line_linkages

 

[Baluncore]

I wonder if there is a possible configuration of that the middle point of that 4 arms mechanism really stays in a vertical line. I can't find the solution now using simple drawings but I feel there should be an easy mathematical proof for it.

There are many approximations to a straight line linkage.
https://en.wikipedia.org/wiki/Straight-line_mechanism
The first exact solution was found in 1864 by Peaucellier.
https://en.wikipedia.org/wiki/Peaucellier–Lipkin_linkage

 

[Baluncore]

Another solution to eliminate friction would be to print the lever and the piston as one part, connected by a short flat ribbon that can flex along its length, or at both ends. The ribbon would stand on a piston crown diameter, and meet the lever at approximately 90°.

A spindle shaped strut could also work, flexing at the ends, but that might be more susceptible to damage, by being twisted off.

 

[Anachronist]

It seems I'm late to the party and you already found a simple solution that works well for what you need.
Still, I just wanted to add that, since your lever is 3D printed you can make the geometries as complex as you like without too much added cost. You could make a lever with a loose wheel at the end so the contact between the piston and the wheel is really rolling instead of an approximation as you initially mentioned in the OP.

Thank you. Yes I was considering something like that until the actual button switches arrived in the mail. They're tiny! Too small to make little wheels reliably 3D printable. The button top is only 4 mm. I didn't realize how small it actually is until I could hold one in my hand and look at it; in my head it was bigger. Also, this isn't a one-off build, it's a manufacturing prototype, likely for injection molding and assembled at a factory, so it's best to minimize the parts required.

Another solution to eliminate friction would be to print the lever and the piston as one part, connected by a short flat ribbon that can flex along its length, or at both ends. The ribbon would stand on a piston crown diameter, and meet the lever at approximately 90°.

A spindle shaped strut could also work, flexing at the ends, but that might be more susceptible to damage, by being twisted off.

In this case, the "piston" is a pre-manufactured button switch (a small thing, like the switches under each key of a computer keyboard). I need to use it as-is, not print it. The part that would be printed is the lever actuator that pushes the switch.

 

[Lnewqban]

Thank you. Yes I was considering something like that until the actual button switches arrived in the mail. They're tiny! Too small to make little wheels reliably 3D printable. The button top is only 4 mm.

Then, the needed stroke should be 0.5 mm at most, and the lever's angular range of motion will be far from 25°.

 

[Anachronist]

Then, the needed stroke should be 0.5 mm at most, and the lever's angular range of motion will be far from 25°.

The stroke is actually 4 mm, with 2 mm being "dead" and the other 2 mm making electrical contact. With a lever pivot about 8 mm away, that's about 26° but I am not planning for the entire stroke to be used.

 

[Lnewqban]

The stroke is actually 4 mm, with 2 mm being "dead" and the other 2 mm making electrical contact. With a lever pivot about 8 mm away, that's about 26° but I am not planning for the entire stroke to be used.

Consider that with that short arm, lateral friction between it and the top of the piston will be transferred down to the switch as a lateral force for which it has not been designed.
It is basically a cam.

 

[Anachronist]

Consider that with that short arm, lateral friction between it and the top of the piston will be transferred down to the switch as a lateral force for which it has not been designed.
It is basically a cam.

For this project I'm assuming here that the lateral force wouldn't be much different from the lateral forces experienced by the switches under a keyboard, in which the forces aren't perfectly axial to the switch. Yes, you're correct, this is basically a cam. Hopefully the curved pad design on the lever (posted earlier) will mitigate the friction and lateral forces somewhat.

 

[Baluncore]

If it was a momentary press-switch, I would solder connections onto the back of the switch PCB, then fake the key press with an analogue gate. Sense the position of the thing that drives the lever and use that information to short the key.

 

[Lnewqban]

You will have 0.25 mm of lateral sliding.

 

[Anachronist]

You will have 0.25 mm of lateral sliding.

Thanks. I managed to redesign it so the rocker lever moves only 17°. There will be some sliding, perhaps mitigated with a bit of lubrication.