Discussion Overview
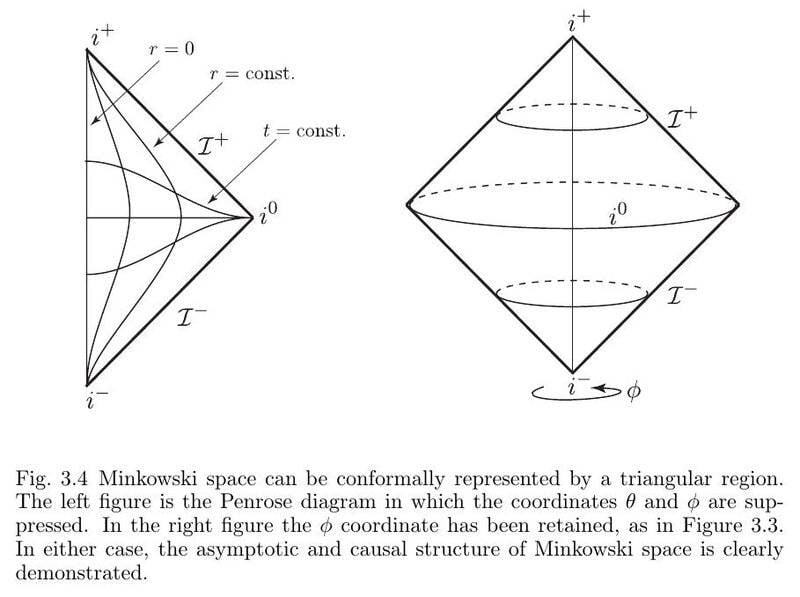
The discussion revolves around the nature of boundaries in Minkowski spacetime in 3+1 dimensions and its conformal diagram, particularly focusing on the line ##r=0## and how it relates to concepts of boundaries in other spacetimes like AdS. Participants explore the implications of these boundaries on causal structures and the representation of worldlines.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
Main Points Raised
- Some participants assert that the Minkowski spacetime does not have a boundary, while the conformal diagram features a timelike boundary at ##r=0##, raising questions about the causal structure differences.
- Others challenge the characterization of ##r=0## as a boundary, suggesting it is a coordinate singularity where worldlines reflect rather than end.
- There is a discussion about the nature of boundaries in Penrose diagrams, with some participants noting that a true boundary is not part of the original spacetime and is added for analysis.
- Some participants propose that the distinction between a true boundary and an apparent one may depend on whether worldlines end or reflect at that location.
- Concerns are raised about the completeness of conformal diagrams in representing the entire spacetime, particularly in relation to spherically symmetric spacetimes.
- Participants discuss the implications of boundaries in AdS spacetime, questioning whether the AdS boundary is part of the original spacetime and how it compares to the ##r=0## line in Minkowski spacetime.
- There is mention of Kerr black holes and the challenges in constructing Penrose diagrams for non-spherically symmetric spacetimes.
- Some participants clarify that for a 4-dimensional spacetime, a boundary must be 3-dimensional, leading to a nuanced understanding of the dimensionality of boundaries in relation to Penrose diagrams.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the nature of ##r=0## and its classification as a boundary or singularity. The discussion remains unresolved with no consensus on the definitions and implications of boundaries in different spacetimes.
Contextual Notes
Limitations include the dependence on definitions of boundaries and singularities, as well as the unresolved nature of how conformal diagrams represent the entirety of spacetime.