Model for a Qubit system using the Hamiltonion Operator

[Lambda96]

Homework Statement

Calculate the eigenvalues and eigenvectors of the Hamilton operator

Relevant Equations

none

Hi,

unfortunately, I am not sure if I have calculated the task a correctly.

I calculated the eigenvalues with the usual formula $\vec{0}=(H-\lambda I) \psi$ and got the following results

$$\lambda_1=E_1=-\sqrt{B^2+\nabla^2}$$
$$\lambda_2=E_2=\sqrt{B^2+\nabla^2}$$

I'm just not sure about the normalized eigenvectors, I got the following as eigenvectors

$$\vec{\psi}_1= \left(\begin{array}{c} \frac{B- \sqrt{B^2+\triangle^2}}{\triangle} \\ 1 \end{array}\right)$$
$$\vec{\psi}_2= \left(\begin{array}{c} \frac{B+ \sqrt{B^2+\triangle^2}}{\triangle} \\ 1 \end{array}\right)$$

For the normalization, I must divide the vectors by their norm. Since writing this vector via Latex is very time-consuming, I have calculated this with Mathematica, instead of the triangle, I have simply written an A. For the eigenvector $\vec{\psi_1}$ I got the following:

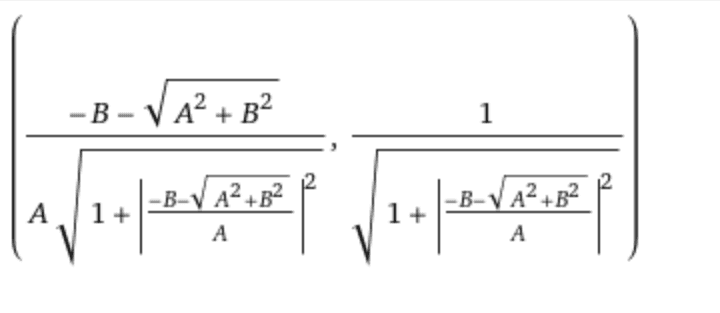
Since this eigenvector looks very messy, I am not sure if I have calculated the task correctly now.

 

[kuruman]

First you need to be less confusing with your symbols. Use \Delta for $\Delta$ and not $\nabla$, $\triangle$ or $A$.
According to our rules, to receive help, you need to show your work. The derivation of the normalized eigenvectors is straightforward but I cannot guide you to it unless I see what what you did. Try to use LaTeX, but if you must use Mathematica, did you know that you can export its equations in LaTeX?

Addendum on edit:
Your expression for $|\psi_1\rangle$ is not correct because it is not a constant times the unnormalized $|\psi_1\rangle$. If you factor out the denominator, you are left with $$
\begin{pmatrix}
\frac{-B-\sqrt{B^2+\Delta ^2}}{\Delta} & 1
\end{pmatrix}$$while the unnormalized vector is
$$
\begin{pmatrix}
\frac{B-\sqrt{B^2+\Delta ^2}}{\Delta} & 1
\end{pmatrix}.$$I suggest that you replace the radical with a single symbol, e.g. $R\equiv \sqrt{B^2+\Delta^2}.$ It will make the algebra more transparent.

 

[Lambda96]

Thanks kuruman for your help

Sorry, because of all the different symbols, unfortunately I still had in mind that it is the Nabla operator $\nabla$. I had then changed all symbols by $\triangle$ and forgotten the change in the eigenvalues. But as you already said correctly, it should be $\Delta$

Try to use LaTeX, but if you must use Mathematica, did you know that you can export its equations in LaTeX?

I did not know that, thanks for the tip
I have now been able to confirm by the following calculation that these are the eigenvectors of A

$$H \vec{\psi}_1=E_1 \vec{\psi}_1$$
$$H \vec{\psi}_2=E_2 \vec{\psi}_2$$

The normalized eigenvectors are then as follows.

$$\hat{\psi}_1=\frac{1}{\sqrt{\biggl( \frac{(B-\sqrt{B^2+\Delta^2})}{\Delta} \biggr)^2+1}} \cdot \left(\begin{array}{c} \frac{B-\sqrt{B^2+\Delta^2}}{\Delta} \\ 1 \end{array}\right)$$

$$\hat{\psi}_2=\frac{1}{\sqrt{\biggl( \frac{(B+\sqrt{B^2+\Delta^2})}{\Delta} \biggr)^2+1}} \cdot \left(\begin{array}{c} \frac{B+\sqrt{B^2+\Delta^2}}{\Delta} \\ 1 \end{array}\right)$$

 

[kuruman]

This is how I would do it.

The unnormalized eigenvector corresponding to $E_1$ is $$|\psi_1\rangle=
\begin{pmatrix}
\frac{B-R}{\Delta} \\
1
\end{pmatrix}~~~R\equiv \sqrt{B^2+\Delta^2}.
$$Let $N$ be the normalization constant by which you must multiply the eigenvector. Then $$\begin{align} 1= & N^2\langle \psi_1 | \psi_1\rangle = \left(\frac{B-R}{\Delta}\right)^2+1= \frac{B^2-2BR+R^2+\Delta^2}{\Delta^2}=\frac{2R^2-2BR}{\Delta^2 }=\frac{2R(R-B)}{\Delta^2} \nonumber \\
& \implies N=\frac{\Delta}{\sqrt{2R(R-B)}}

\nonumber \end{align}$$and the normalized eigenvector is
$$|\psi_1\rangle=\frac{1}{\sqrt{2R(R-B)}}
\begin{pmatrix}
{B-R} \\
\Delta
\end{pmatrix}.
$$The normalized eigenvector corresponding to $E_2$ is obtained by swapping the column vector elements and introducing a relative minus sign. Obviously, the overall phase doesn't matter.
$$|\psi_2\rangle=\frac{1}{\sqrt{2R(R-B)}}
\begin{pmatrix}
-\Delta \\
B-R
\end{pmatrix}.$$It is immediately clear that the above vectors are orthonormal. In your expression that is not obvious. That is what I meant when I said that the substitution $R=\sqrt{B^2+\Delta^2}$ in such problems makes the algebra transparent.

 

[Lambda96]

Thanks again kuruman for your help and for the tip with the calculation of the normalization constant $N$ .

I would have only one question, concerning the normalized eigenvector $\hat{\psi}_2$.

I would have now calculated the normalization constant exactly as for $\hat{\psi}_1$ and got the following

$$N=\frac{\Delta}{\sqrt{2R(R+B)}}$$

I would then get the following as the normalized eigenvector.

$$\hat{\psi}_2=\frac{\Delta}{\sqrt{2R(R+B)}} \cdot \left(\begin{array}{c} B+R \\ 1 \end{array}\right)$$

Unfortunately, I don't quite understand why I also get the eigenvector when I swap the columns for the normalized eigenvector $\hat{\psi}_1$ and multiply by minus. I wanted to verify with the calculation $H\hat{\psi}_2=E_2 \hat{\psi}_2$ that it is an eigenvector of H and unfortunately I got the following.

$$H \cdot \left(\begin{array}{c} -\Delta \\ B-R \end{array}\right)=\frac{\Delta}{\sqrt{2R(R+B)}} \cdot \left(\begin{array}{c} -\Delta R\\ -\Delta^2-B(B-R) \end{array}\right)$$

The first line is correct, only with the second line I have problems.

Is it possible to determine the normalized eigenvectors of a 2x2 matrix with this trick, or only in certain cases?

 

[kuruman]

First of all this $$\hat{\psi}_2=\frac{\Delta}{\sqrt{2R(R+B)}} \cdot \left(\begin{array}{c} B+R \\ 1 \end{array}\right)$$is dimensionally incorrect. The first element in the column vector has dimensions of energy while the second element is dimensionless. That cannot be. Also, I think you should have a term $(R-B)$ in the denominator, not $(R+B).$ Recheck your work.

Is it possible to determine the normalized eigenvectors of a 2x2 matrix with this trick, or only in certain cases?

It is possible to use this trick with any 2×2 matrix. In the more general case where the eigenvectors have complex coefficients, let the normalized eigenvectors be
$|\psi_1\rangle=a_1|1\rangle +b_1|2\rangle~~~(|a_1|^2+|b_1|^2=1).$
$|\psi_2\rangle=a_2|1\rangle +b_2|2\rangle~~~(|a_2|^2+|b_2|^2=1).$
To ensure that they are orthogonal, you must have
$$0=\langle\psi_2|\psi_1\rangle=
\begin{pmatrix}
{a^*_2} & b^*_2
\end{pmatrix}
\begin{pmatrix}
{a_1} \\ b_1
\end{pmatrix}=a^*_2a_1+b^*_2b_1.
$$Once you obtain $a_1$ and $b_1$ for the first eigenvector, you can immediately write $a_2\rightarrow -b^*_1$ and $b_2\rightarrow a^*_1$ because then $$a^*_2a_1+b^*_2b_1\rightarrow (-b^*_1)^*a_1+ (a^*_1)^*b_1=-b_1a_1+a_1b_1=0.$$Of course, if the coefficients are real as in this case, you don't have to worry about the complex conjugates, just swap elements and introduce a relative negative sign.

 

[Lambda96]

Thanks kuruman for your help and your explanation for finding the eigenvectors of a 2x2 matrix, for future tasks, this will simplify the calculation