FabusMarco
- 2
- 0
Hello,
I was solving a problem related to Eddie currents recently and I need some help with simulating it numerically. Basically, we have a disc-like copper pendulum entering a region of uniform magnetic flux density B (see diagram). I understand that I need to use Faraday's law:
\nabla \times \vec{E} = - \frac {\partial{\vec B}} {\partial t},
but even if I assume B is in the z-direction and E is in the x-y plane, I am left with
\frac {\partial{E_y}} {\partial x} - \frac {\partial{E_x}} {\partial y} = - \frac {\partial{B}} {\partial t}.
Once I have E, I can find J and subsequently the current induced. However, do I not have too many variables? And how could I then find the retarding force, given that it depends on things like the velocity of moving charges?
Many thanks for your help in advance.
Diagram:
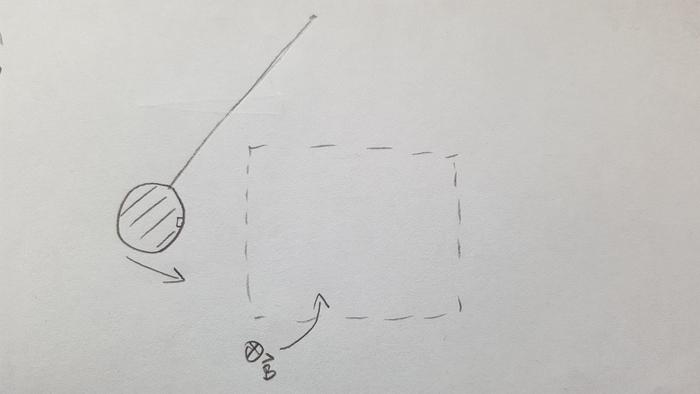
I was solving a problem related to Eddie currents recently and I need some help with simulating it numerically. Basically, we have a disc-like copper pendulum entering a region of uniform magnetic flux density B (see diagram). I understand that I need to use Faraday's law:
\nabla \times \vec{E} = - \frac {\partial{\vec B}} {\partial t},
but even if I assume B is in the z-direction and E is in the x-y plane, I am left with
\frac {\partial{E_y}} {\partial x} - \frac {\partial{E_x}} {\partial y} = - \frac {\partial{B}} {\partial t}.
Once I have E, I can find J and subsequently the current induced. However, do I not have too many variables? And how could I then find the retarding force, given that it depends on things like the velocity of moving charges?
Many thanks for your help in advance.
Diagram: