Moment of forces about the axes

[mingyz0403]

Homework Statement:

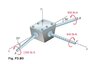
Shafts A and B connect the gear box to the wheel assemblies of a tractor, and shaft C connects it to the engine. Shafts A and B lie in the vertical yz plane, while shaft C is directed along the x axis. Replace the couples applied to the shafts by a single equivalent couple, specifying its magnitude and the direction of its axis.

Relevant Equations:

M=RXF

I reslove Ma and Mb into y and z component.
Ma=1200sin(20)j+1200cos(20)k
Mb=900sin(20)j+1200cos(20)k
Mc=-840i

I looked at the solution and it states that the y component of Ma is negative (-1200sin(20)j+1200cos(20)k). I understand that Mc is -840i because it is Clockwise. How do you determine the sign of Ma and Mb for their y and z component.

Many times for your time answering my question.

 

[PhanthomJay]

It is best to forget about sign conventions for clockwise and counterclockwise. Rather, show the couple in its vector form using the right hand rule , and the moment vector will point in the direction of your thumb. Then you should be able to more easily find the projection and signage of the vector Components onto the y and z axes. Hint: the couple about the x-axis is negative because it points in the negative x direction.

 

[FactChecker]

The A-torque is tilted slightly down, in the -y direction. Using the right-hand rule, it is positive when looked at in the -y direction. That is the same as negative in the +y direction. The B-torque is tilted slightly up in the +y direction.