- #1
ahmed markhoos
- 49
- 2
The hoop has radius R.
I used the same way to plot the axis for the hoop:
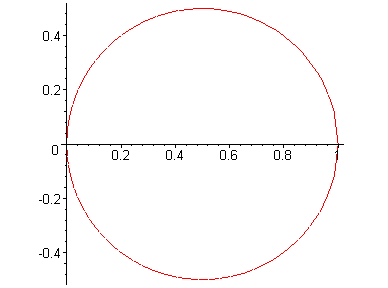
##l^2 = r^2= 4R^2cos\theta##
since: ##r=2Rcos\theta##
[tex]2\rho \int_{0}^{\frac{\pi}{2}} r^2 r d\theta[/tex]
[tex]2\rho \int_{0}^{\frac{\pi}{2}} 8R^3 cos^3\theta d\theta[/tex]
answer is [tex]\frac{32}{3}R^3\rho[/tex] , and its wrong
using the same method to find mass is also wrong, which suggest a fundamental mistake in my solution but I don't know what it is.
[tex]2\rho \int_{0}^{\frac{\pi}{2}} r d\theta[/tex]
[tex]2\rho \int_{0}^{\frac{\pi}{2}} 2R cos\theta d\theta[/tex]
that's equal [tex]4\pi r[/tex] which is wrong
what is wrong with my solution?, it was really bizarre when I found that the mass itself using the limits I found actually gives a wrong answer.
What did I miss?
I used the same way to plot the axis for the hoop:
##l^2 = r^2= 4R^2cos\theta##
since: ##r=2Rcos\theta##
[tex]2\rho \int_{0}^{\frac{\pi}{2}} r^2 r d\theta[/tex]
[tex]2\rho \int_{0}^{\frac{\pi}{2}} 8R^3 cos^3\theta d\theta[/tex]
answer is [tex]\frac{32}{3}R^3\rho[/tex] , and its wrong
using the same method to find mass is also wrong, which suggest a fundamental mistake in my solution but I don't know what it is.
[tex]2\rho \int_{0}^{\frac{\pi}{2}} r d\theta[/tex]
[tex]2\rho \int_{0}^{\frac{\pi}{2}} 2R cos\theta d\theta[/tex]
that's equal [tex]4\pi r[/tex] which is wrong
what is wrong with my solution?, it was really bizarre when I found that the mass itself using the limits I found actually gives a wrong answer.
What did I miss?
Last edited:

