Moment of Inertia of a Square: Problem with Certain Method

[DocZaius]

For fun, I thought I would try to derive the moment of inertia of a square using different approaches (in each case, changing the differential area being integrated). Everything went well until I tried the approach of first considering the disk in the center of the square, then adding the bits at the corners.

Consider a square with sides of length L. The moment of inertia of the disk of radius L/2 in the center is:

I_{disk}=\frac{1}{2}MR^2=\frac{1}{2}M({\frac{L}{2}})^2=\frac{1}{8}ML^2

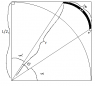
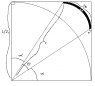
Now consider a corner of the square (attached image). If we figure out the contribution to the moment of inertia of that corner, we can account for the others by multiplying it by 4 because of radial symmetry. We will take arcs with differential thickness from the edge of the circle to the very corner of the square and add up their contributions to the moment of inertia. Here is the formula for the differential area:

<br /> \cos(\alpha)=\frac{\frac{L}{2}}{r}\\<br /> \theta=\frac{\pi}{2}-2\alpha\\<br /> \theta=\frac{\pi}{2}-2\arccos(\frac{L}{2r})\\<br /> \\<br /> da=r\,\theta\,dr\\<br /> da=r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr<br />

Now the integral for the contribution of the corner to the moment of inertia is:

<br /> \rho=\frac{M}{A}=\frac{M}{L^2}=\frac{dm}{da}\\<br /> dm=\rho\,da=\rho \, r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr\\<br /> I_{corner}=\int_M r^2 \, dm=\int_{\frac{L}{2}}^{\frac{\sqrt{2}}{2}L} r^2 \, \rho \, r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr\\<br />
Which leads to the following for the total moment of inertia:
<br /> I_{square}=I_{disk}+4\,I_{corner}=\frac{1}{8}ML^2+4 \int_{\frac{L}{2}}^{\frac{\sqrt{2}}{2}L} r^2 \, \rho \, r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr<br />
My problem is that the integral for the moment of inertia of a corner does not give me what it should (\frac{1}{96}ML^2) but rather gives me something with pi in it. I cannot figure out at what point I went wrong. Can someone see the error?

Thanks.

edit: Despite this not being homework, I realize it might belong in the homework forum. I wasn't sure and went with this forum. Mods, please move it if it needs to be moved.

 

[OldEngr63]

I have not worked through the whole problem, but one place that looks suspect is the use of M. I see M as the mass of the disk, and the same symbol appearing again in the definition of rho for the corner MMOI calc. I think this may be part of your problem.

 

[DocZaius]

I have not worked through the whole problem, but one place that looks suspect is the use of M. I see M as the mass of the disk, and the same symbol appearing again in the definition of rho for the corner MMOI calc. I think this may be part of your problem.

Thank you! That might just be it.

 

[mathman]

What do you have for the integral of the term involving arccos?

 

[DocZaius]

That was it! Sorry mathman - I can't quite answer your question properly at the moment, but I plugged everything into wolfram alpha with M=L=1 and I got the right answer! (1/6 ML^2)

How funny that the bit I got wrong was in the easiest part of the derivation.

 

[DocZaius]

To follow up on mathman's question (in case he still cares), the integral of the term involving arcos is:

\int_{\frac{L}{2}}^{\frac{\sqrt{2}}{2}L} r^2 \, \rho \, r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr=\frac{1}{384}ML^2(16-3\pi)
where I plugged in \rho=\frac{M}{L^2}

 

[mathman]

I am confused. Your last 2 posts seem to contradict each other. One says you got the right answer, the other says the integral has a term involving π.

 

[mfb]

The integral has to have pi as part of its answer. The inner part has a pi-contribution as well (hidden in its area<->mass), and the final result for the square is rational.

 

[DocZaius]

The integral has to have pi as part of its answer. The inner part has a pi-contribution as well (hidden in its area<->mass), and the final result for the square is rational.

That's exactly right. Initially (post #1), I thought that I should not have pi in the integral involving arccos since my moment of inertia term for the circle did not have one. The reason I thought that was because my final answer needed to be rational: (1/6)ML^2. Therefore I thought my error had to do with the arccos integral yielding a pi. However, OldEngr63 pointed out that my error did not lie with my integral but instead came from the fact that I was using the wrong mass for the circle at the very beginning of my derivation. With the correct circle moment of inertia (which must have a pi in it when taken as a portion of the square's mass!) I now needed a pi in my arccos integral. But I always and correctly had it there! Thanks all.

 

[DocZaius]

Here is the corrected derivation:

To find the moment of inertia of a square: Consider a square with sides of length L. The moment of inertia of the disk of radius L/2 in the center is:

I_{disk}=\frac{1}{2}M_{disk}R^2=\frac{1}{2}(\frac{\pi R^2}{L^2}M_{square})R^2=\frac{1}{2}\frac{\pi (\frac{L}{2})^2}{L^2}M_{square}(\frac{L}{2})^2=\frac{1}{2}\frac{\pi}{4}M_{square}(\frac{L}{2})^2=\frac{\pi}{32}M_{square}L^2

Where M_{square}=M from now on. Now consider a corner of the square (attached image). If we figure out the contribution to the moment of inertia of that corner, we can account for the others by multiplying it by 4 because of radial symmetry. We will take arcs with differential thickness from the edge of the circle to the very corner of the square and add up their contributions to the moment of inertia. Here is the formula for the differential area:

<br /> \cos(\alpha)=\frac{\frac{L}{2}}{r}\\<br /> \theta=\frac{\pi}{2}-2\alpha\\<br /> \theta=\frac{\pi}{2}-2\arccos(\frac{L}{2r})\\<br /> \\<br /> da=r\,\theta\,dr\\<br /> da=r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr<br />

Now the integral for the contribution of the corner to the moment of inertia is:

<br /> \rho=\frac{M}{A}=\frac{M}{L^2}=\frac{dm}{da}\\<br /> dm=\rho\,da=\rho \, r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr\\<br /> I_{corner}=\int_{M_{corner}} r^2 \, dm=\int_{\frac{L}{2}}^{\frac{\sqrt{2}}{2}L} r^2 \, \rho \, r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr\\<br />
Which leads to the following for the total moment of inertia:
<br /> I_{square}=I_{disk}+4\,I_{corner}=\frac{\pi}{32}ML^2+4 \int_{\frac{L}{2}}^{\frac{\sqrt{2}}{2}L} r^2 \, \rho \, r(\frac{\pi}{2}-2\arccos(\frac{L}{2r}))dr=\frac{\pi}{32}ML^2+\frac{4}{384}ML^2(16-3\pi)=\frac{1}{6}ML^2<br />
where \rho=\frac{M}{L^2}

 

[mathman]

I(square)=ML²/6 . I don't understand your result.

 

[DocZaius]

I(square)=ML²/6 . I don't understand your result.

I was trying to find the moment of inertia of a (filled) square about its center. The answer to that is \frac{1}{6}ML^2. There are a few different ways to work it out, but the method I chose was to first find the moment of inertia for the disk contained in the square, and then do the corners. My most recent post above this one is that derivation. I arrive at the correct answer. Please let me know what you don't understand.

 

[mathman]

Problem was with my web page display. Your typography is very large, so the right end of the expression was chopped off.