Momentum at time t and at a time t+dt for a rocket

[mcastillo356]

Hello, my name is Marcos, I have a bachelor in advertising and public relations, and my hobby is maths and physics
The equation of variable-mass motion is written as $\mathbf{F}_{ext}+\mathbf{v}_{rel}\dfrac{dm}{dt}=m\dfrac{d\mathbf{v}}{dt}$
There are different derivations for the equation:
Mass accretion:

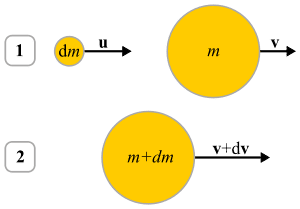
Mass ablation/ejection:

The initial momentum of the system is $\mathbf{p}_1=m\mathbf{v}$. Since the mainbody will be losing mass, $dm$ will be negative. At a time $t+dt$ the momentum is $\mathbf{p}_2=(m+dm)(\mathbf{v}+d\mathbf{v})+\mathbf{u}(-dm)$. Why in the same equation $dm$ is first positive and at the end negative?.
Full text at https://en.wikipedia.org/wiki/Variable-mass_system
Thanks!

 

[Orodruin]

Since dm is negative, m+dm < m and -dm > 0. dm itself is negative, it does not change sign.

Since dm is the mass gained by the rocket (being negative means the rocket loses mass), the mass of the ejecta is -dm.

 

[PeroK]

Why in the same equation $dm$ is first positive and at the end negative?.

It's not positive and negative in the same equation. $dm$ is whatever it is. Your question is really: "Why in the equation do we use $+dm$ in one place and $-dm$ in another? Or, why do we sometimes add $dm$ and sometimes subtract it?

To answer this, consider this equation, for example:

$a + b = (a + c) + (b - c)$

 

[mcastillo356]

Thank you very much, Orodruin and Perok!. Question solved

 

[mcastillo356]

Hello
The general equation of variable-mass motion is written as $\mathbf{F}_{ext}+\mathbf{v}_{rel}\dfrac{dm}{dt}=m\dfrac{d\mathbf{v}}{dt}$, where $\mathbf{F}_{ext}$ is the net external force on the body, $\mathbf{v}_{rel}$ is the relative velocity of the escaping or incoming mass with respect to the center of mass of the body, and $\mathbf{v}$ is the velocity of the body

Noting that $\mathbf{u}-\mathbf{v}$ is the velocity of $dm$ relative to $m$, simbolized as $\mathbf{v}_{rel}$
The question is: velocity of $dm$ and $m$, is relative to Earth?
Thanks!

 

[Dale]

It is relative to any inertial reference frame. The Earth is a good example, but any other inertial frame will do just as well too.

 

[mcastillo356]

Hello!
Is the geogebra file I've attached the momentum for a rocket in motion at a time $t$ and at a time $t+dt$?. I've done it inspired by

witch shows mass accretion for a variable-mass system.
Thanks!

 

[mcastillo356]

Thank you very much, Dale

 

[mcastillo356]

Hello Orodruin
The pdf I attached drawing mass ablation for a variable-mass system like a rocket was not wright. I am student of spanish Uned, I am preparing a specific entrance exam to access maths degree. The image I've drawn is their advice. The system taken in account is the rocket and the fuel yet to burn. Thanks!

At time t it's m with velocity vector v, in the left; and in the right, at time t+dt, it's the rocket, with mass m-dm and velocity vector v+dv, and below, dm, with velocity vector u downwards, to preserve momentum