- #1
duran9987
- 12
- 2
Homework Statement
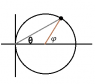
A particle moves with constant speed ν around a circle of radius b, with the circle offset from the origin of coordinates by a distance b so that it is tangential to the y axis. Find the particle's velocity vector in polar coordinates.
Homework Equations
(dots for time derivatives are a bit off centered)[/B]Position Vector:
r = r ˆr
Velocity Vector:
v = ˙r ˆr + r ˙ θˆθ
Angular Speed:
ω = ˙ θ →(Integrating with respect to time)→ ωt = θ
v = bω → ω = v/b
The Attempt at a Solution
I found the equation of the graph to be r = 2bcosθ.
Differentiating with respect to time i get
˙r = -2bsinθ˙ θ → ˙r = -2bωsinωt.
Substituting the into the velocity vector i obtain:
v = -2bωsinωtˆr + 2bωcosωtˆθ
= -2vsin(vt/b)ˆr + 2vcos(vt/b)ˆθ
what am i doing wrong here?, the book uses a confusing approach (confusing to me). For the velocity vector they have…
v = −v sin(vt/2b)ˆr + v cos(vt/2b)ˆθ
any help will be greatly appreciated.