Motion On An Off Center Circle In Polar Coordinates

[duran9987]

Homework Statement

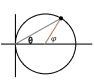
A particle moves with constant speed ν around a circle of radius b, with the circle offset from the origin of coordinates by a distance b so that it is tangential to the y axis. Find the particle's velocity vector in polar coordinates.

Homework Equations

(dots for time derivatives are a bit off centered)[/B]
Position Vector:
r = r ˆr
Velocity Vector:
v = ˙r ˆr + r ˙ θˆθ
Angular Speed:
ω = ˙ θ →(Integrating with respect to time)→ ωt = θ
v = bω → ω = v/b

The Attempt at a Solution

I found the equation of the graph to be r = 2bcosθ.
Differentiating with respect to time i get
˙r = -2bsinθ˙ θ → ˙r = -2bωsinωt.

Substituting the into the velocity vector i obtain:
v = -2bωsinωtˆr + 2bωcosωtˆθ
= -2vsin(vt/b)ˆr + 2vcos(vt/b)ˆθ

what am i doing wrong here?, the book uses a confusing approach (confusing to me). For the velocity vector they have…

v = −v sin(vt/2b)ˆr + v cos(vt/2b)ˆθ

any help will be greatly appreciated.

 

[TSny]

Don't confuse the polar coordinate θ with the angle φ, say, that the radius of the circle makes to the horizontal.

Does v = b dθ/dt or does v = b dφ/dt?

 

[duran9987]

Don't confuse the polar coordinate θ with the angle φ, say, that the radius of the circle makes to the horizontal.

Does v = b dθ/dt or does v = b dφ/dt?

Thanks for the response!

Don't confuse the polar coordinate θ with the angle φ, say, that the radius of the circle makes to the horizontal.

Does v = b dθ/dt or does v = b dφ/dt?

Hello TSny, thank you for the reply. So just to clarify, when i am evaluating the vector in polar coordinates i should always consider the angle between the radius of the circle and the horizontal, not the angle that the position vector makes with the horizontal??

 

[haruspex]

Hello TSny, thank you for the reply. So just to clarify, when i am evaluating the vector in polar coordinates i should always consider the angle between the radius of the circle and the horizontal, not the angle that the position vector makes with the horizontal??

You may need to consider both angles, just be aware that they are different. The theta in the polar coordinates refers to the angle the position vector makes with the horizontal.
In your equations, you have equated $\omega$ with $\dot{\theta}$, but taken it to be the constant rate of rotation about the circle's centre, which would make it $\dot{\phi}$.

 

[ehild]

You get r=2bcosθ for the equation of the graph in polar coordinates. What happens if cosθ is negative? Don't you miss something in the equation?
As for the velocity in the polar coordinates r and θ: See picture. Can you find a relation between the angles θ and Φ? What angle does the velocity vector v make with the unit vectors of the (R, θ) polar coordinate system? What are its components in that system?

Remember the speed is V along the circle. So the angular velocity is V/b with respect to the centre of the circle, but dθ/dt is not equal to it.

 

[duran9987]

You get r=2bcosθ for the equation of the graph in polar coordinates. What happens if cosθ is negative? Don't you miss something in the equation?
As for the velocity in the polar coordinates r and θ: See picture. Can you find a relation between the angles θ and Φ? What angle does the velocity vector v make with the unit vectors of the (R, θ) polar coordinate system? What are its components in that system?

Remember the speed is V along the circle. So the angular velocity is V/b with respect to the centre of the circle, but dθ/dt is not equal to it.View attachment 87578

This clears a lot up for me. Thank you very much. I see that Φ = 2θ and can now make sense of the books equations. But I am thinking of your question about negative cosθ.. for values of 0 ≤ θ ≤ π .. 2bcosθ just traces the graph… I'm not sure what the equation is missing.

 

[ehild]

The radius is positive. How to make a negative number positive and of the same magnitude?

 

[Monish Mohonto]

why the angular velocity is counting from the basis of the x,y origin where the particle is moving along the circle?why we are not counting the angular velocity from the origin of the circle??

 

[Chestermiller]

The key to this problem is expressing the position vector from the origin in terms of b and $\theta$:
$$\vec{r}=2b\cos{\theta}\ \vec{i}_r$$
and recognizing that $\theta = \phi /2$ so that$$\frac{d\theta}{dt}=\omega/2$$

 

[Monish Mohonto]

Thank you for your co-operation.