- #1
avcireis
- 22
- 0
Hello,
Short description: In my country's physics olympics, if a loop of wire is moved in a changing magnetic field, the time derivative of the area (while calculating emf with lenz law) is the velocity of the loop (as if we're taking the time derivative of the AREA SWEPT).
This has became an axiom for me right now. I do the questions based on this and they are correct, so no problem practically. I am just wondering why.
Here's an example question and its solution if I wasn't clear enough.

The loop is moving with acceleration a in the magnetic field defined. Find emf as a function of time
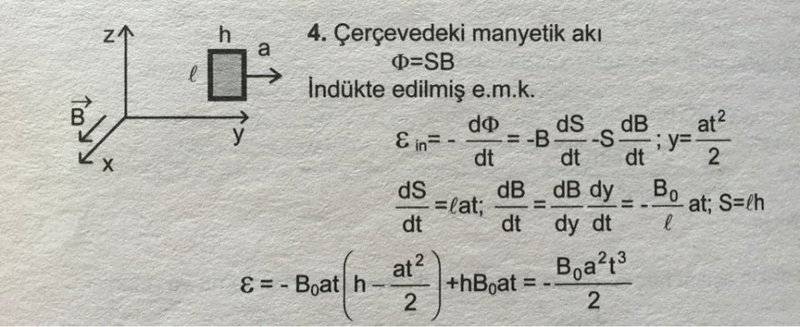
What I'm talking about happens in the beginning of the third line of equations.
Thank you
Short description: In my country's physics olympics, if a loop of wire is moved in a changing magnetic field, the time derivative of the area (while calculating emf with lenz law) is the velocity of the loop (as if we're taking the time derivative of the AREA SWEPT).
This has became an axiom for me right now. I do the questions based on this and they are correct, so no problem practically. I am just wondering why.
Here's an example question and its solution if I wasn't clear enough.
The loop is moving with acceleration a in the magnetic field defined. Find emf as a function of time
What I'm talking about happens in the beginning of the third line of equations.
Thank you