Feodalherren
- 604
- 6
Homework Statement
Homework Equations
The Attempt at a Solution
Umm can somebody explain to me what just happened. None of that makes any sense to me what so ever.
This discussion focuses on the application of the chain rule in multivariable calculus, specifically in the context of partial derivatives. Participants clarify the notation and concepts surrounding the composition of functions, denoted as ##F \circ G##, where ##G(s,t) = (u(s,t), v(s,t))##. The chain rule is emphasized as a method to compute derivatives of composite functions, leading to the expression for ##\frac{\partial W}{\partial s}##. The conversation highlights the confusion around notation and the necessity of understanding the underlying functions involved.
PREREQUISITESStudents and educators in mathematics, particularly those studying or teaching multivariable calculus, as well as anyone seeking to improve their understanding of partial derivatives and the chain rule.
Feodalherren said:Ok I have no idea.. I can't remember what FoG means :/. You didn't even define F as anything?
Feodalherren said:Homework Statement
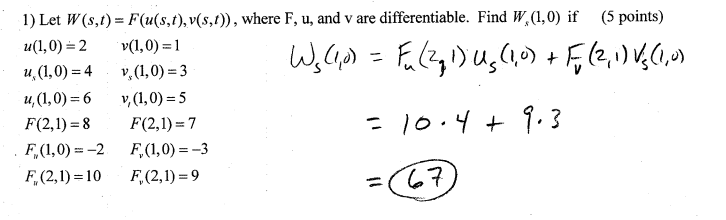
Homework Equations
The Attempt at a Solution
Umm can somebody explain to me what just happened. None of that makes any sense to me what so ever.