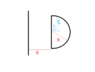The symbol x has a different meaning in the two integrals. In post #11, you were letting x represent the distance shown here:
View attachment 251815But, in post #14, x represents the distance shown here:
View attachment 251816
Suppose we use a capital X for your distance in post 11 and a lower case x for the distance shown for post 14. Then your integral in post 11 would look the same except for using X instead of x. To get the integral for post 14, you need to change the variable of integration from X to x. What is the relation between X and x? Use this as a substitution to get from the integral in 11 to the integral in 14. Also, be sure to include the limits for the integrals.