Mutual Inductance between two conductors

[Jason-Li]

Homework Statement

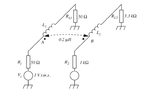
The mutual inductance between two circuits as shown is 0.2 μH.
It may be assumed that (R1 + RL1) >> ωL1 and that (R2 + RL2) >>ωL2.

(a) Estimate the crosstalk voltage at the load of circuit B when the signal
source of circuit A is V1 = 1 V at 1 GHz.

(b) Plot the crosstalk voltage (at the load of circuit B) as a function of
frequency.

Relevant Equations

(R1 + RL1) >> ωL1 and (R2 + RL2) >>ωL2.

Hello hope everyone at PF are keeping well!

Looking at this problem but don't know if I have oversimplified it and my final answer doesn't seem right?
So I drew the equivalent circuit:

Then went onto calculate:
I1 = 1/(R₁+R_L1) = 0.01A
ω = 2πf = 2π*10⁹ rads^-1
so then with V_i being the inducted voltage:
V_i = jω * M * I₁ = 2π*10⁹ * 0.2*10^-6*0.01 = 12.566V This seems a bit high?

I also did the classic ohms law and did V_L2 = V_i / (R₂+R_L2) * R₂ = 9.643V to get the answer for (a)? I am really unsure if I have approached this correctly, any help would be greatly appreciated.

Then for part (b) I was just going to plot a straight line as the function is
V_i= jω*M*I₁ I would change this to
V_i = (2π*M*I₁)*f which is the same as y=mx ?

 

[tech99]

I think the primary current is flowing through M, which has a large reactance. So I1 = V1/omega M (approx).

 

[Jason-Li]

I think the primary current is flowing through M, which has a large reactance. So I1 = V1/omega M (approx).

I think as it's mutual inductance current I1 won't be altered by M, but will effect M?

I have calculated I1 and then from that I can calculate the mutual inducted voltage?