Discussion Overview
The discussion revolves around the representation of gravity in the context of relativity, particularly critiquing the common analogies used, such as the rubber sheet model. Participants express concerns about these representations and explore alternative ways to conceptualize how warped space influences the motion of objects.
Discussion Character
- Debate/contested
- Conceptual clarification
- Exploratory
Main Points Raised
- Some participants argue that the rubber sheet analogy is inadequate, suggesting it implies a separate source of gravity pulling objects downward, which they find misleading.
- Others propose that analogies are inherently flawed but can still serve as useful tools for understanding complex concepts, though they caution against relying too heavily on them.
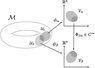
- A participant mentions that the rubber sheet model leads to confusion and suggests alternative representations, such as A.T.'s graphics or the analogy of ants on an apple, which they find more effective.
- There is a discussion about the mathematical foundations of gravity, with some asserting that a deeper understanding requires engaging with the mathematics of the subject.
- One participant critiques the common descriptions accompanying the rubber sheet model, arguing that they misrepresent the physics involved, particularly regarding the motion of objects in gravitational fields.
- Another participant humorously suggests imagining a cosmic hand pushing objects into the fabric of space, indicating a playful approach to the discussion.
Areas of Agreement / Disagreement
Participants express a range of opinions, with some agreeing on the inadequacy of the rubber sheet analogy while others defend the use of analogies in general. The discussion remains unresolved regarding the best way to represent gravity and the implications of these representations.
Contextual Notes
Participants highlight limitations in the rubber sheet analogy, including its failure to accurately convey the dynamics of gravity and the potential for misunderstandings. There are also references to mathematical concepts that underpin the discussion, suggesting a need for clarity in how these models are presented.
Who May Find This Useful
This discussion may be of interest to individuals exploring the conceptual foundations of gravity, those studying relativity, and anyone engaged in discussions about the effectiveness of scientific analogies.