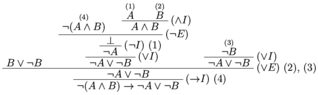Natural Deduction: Solving Sequents [7/10]

  • MHB
  • Thread starter Mia Fuller
  • Start date
  • Tags
    Natural
In summary, the conversation is about completing natural deduction proofs for two sequents. The first sequent is ¬ (P ˅ Q), R → P and the second sequent is (P & Q) → ¬ R. The numbers in brackets indicate that each proof should be 7 or 10 lines long. The person asking for help also mentions using a Fitch-style calculus for the proofs. They have attempted both proofs but have not been able to keep them within the specified number of lines. They ask for any help and thank the person in advance.
  • #1
Mia Fuller
1
0
Hi guys, does anyone know how to complete proofs of natural deduction for these sequents? ¬ (P ˅ Q), R → P : ¬ R [7]

(P & Q) → ¬ R, : R → (P → ¬ Q) [10]the {7} in brackets indicates how many lines each answer should be. I attempted both but my amount of lines were not 7 or 10

Would really appreciate any help. Thank you
 
Physics news on Phys.org
  • #2
If we are talking about the number of lines, then we should describe the inference rule more precisely. After all, the following derivation is also natural deduction (in tree form).


I assume you are using the so called Fitch-style calculus. Then you can have something like the following.

Code: 
   R
   R -> P
   P
   P \/ Q
   ~(P \/ Q)
   _|_
~R

By \(\displaystyle \bot\) I denote contradiction. You may have a different rule for deriving negations.

You could post your attempt at the second derivation, and we can discuss it.
 

Attachments

  • natutal-deduction.png
    natutal-deduction.png
    5.1 KB · Views: 70

FAQ: Natural Deduction: Solving Sequents [7/10]

What is natural deduction?

Natural deduction is a logical system used to derive conclusions from given premises. It is based on the idea of constructing proofs by using a set of rules and principles, rather than relying on truth tables or other methods. It is commonly used in the field of mathematical logic and is considered a fundamental tool for deductive reasoning.

How does natural deduction work?

Natural deduction works by using a set of logical rules and principles to systematically break down a given argument or statement into smaller parts, eventually leading to a conclusion. These rules include the introduction and elimination of logical connectives, as well as the use of assumptions and logical equivalences. The goal is to show that the conclusion can be derived from the given premises by following these rules.

What is a sequent in natural deduction?

A sequent is a statement in the form of A1, A2, ..., An ⊢ B, where A1, A2, ..., An are the premises and B is the conclusion. It is a representation of a logical argument or proof, and the goal is to show that the conclusion B can be derived from the premises A1, A2, ..., An using the rules of natural deduction.

What is the purpose of solving sequents in natural deduction?

The purpose of solving sequents in natural deduction is to demonstrate that a given conclusion can be derived from a set of premises using logical principles. It allows us to determine the validity of arguments and identify any potential logical fallacies. Solving sequents also helps us to better understand the structure and relationships between different propositions and logical connectives.

How is natural deduction used in scientific research?

Natural deduction is a valuable tool in scientific research as it allows for the systematic evaluation of arguments and hypotheses. By using logical rules and principles, scientists can identify and eliminate any potential flaws or inconsistencies in their reasoning. Natural deduction also helps to establish the validity of scientific theories and support the development of new ideas and theories through deductive reasoning.

Similar threads

MHB Natural deduction (negated implication)
Replies
8
Views
3K
MHB Stuck on Derivation (Natural Deduction)
Replies
1
Views
1K
MHB Understanding Ke Logic Rules & Finding Contradictions
Replies
4
Views
2K
MHB How Do I Apply Natural Deduction to These Logic Problems?
Replies
2
Views
2K
MHB Getting Nowhere with a Proof Question: Help Needed
Replies
3
Views
2K
B Unbounded Logical Trees: Constructing Natural Numbers with Logical Trees
Replies
7
Views
2K
MHB Universal Quantifier Intro: Natural Deduction in Predicate Logic
Replies
9
Views
4K
MHB Expanding Brackets: Math Help for 2nd Term Maths
Replies
4
Views
1K
I Why Does This Mathematical Proof Seem Flawed?
Replies
18
Views
2K
I Counterexample Required (Standard Notations)
Replies
16
Views
2K

Hot Threads

Recent Insights

Back
Top