alexf322
- 5
- 0
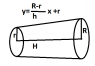
Homework Statement
For calc 2 we have to write a formula using integration that will find the volume of any tree log that is cut. Using the picture that is attacked I came up with this equation. The integral from 0 to h of pi*(((R-r/h)x+r))^2)dx. Any ideas about my formula or anything would be appreciated. Thanks