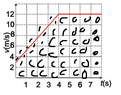
The discussion revolves around interpreting a velocity-time graph to determine the distance traveled by an object and its acceleration over specified time intervals. The subject area includes kinematics and the relationships between velocity, acceleration, and position.
The conversation is ongoing, with participants offering guidance on how to approach the problems. Some have provided specific calculations and interpretations of the graph, while others are still seeking clarity on their methods and results.
Participants have noted the need to show their work and clarify their approaches to receive assistance. There is a focus on understanding the definitions and relationships between speed, velocity, and acceleration as they relate to the graph.
Yes, in a velocity-time graph the distance traveled is given by the 'area' under the graph line. But the area of each square means the product of the coordinate intervals.gladidi said:
That is the right answer. I cannot tell whether you are expected to do it by counting squares are algebraically. I would use standard formulae for areas of rectangles and triangles.gladidi said:
35*2+8/2*2? is 78m but it's not right..haruspex said:
You want the distance for the whole 8 seconds, right?gladidi said:
