Need help with understanding this solution (fluid pressure problem)

[bigmike94]

TL;DR

I dont fully understand the solution

So here’s the question (I am only talking about the pressure at point B, the other 2 I can understand.)

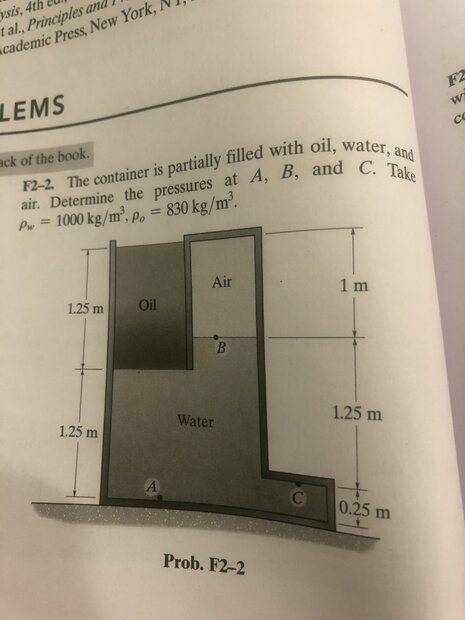
And here is the solution

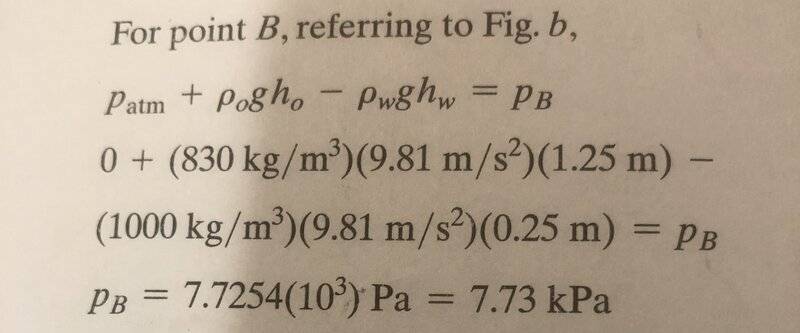
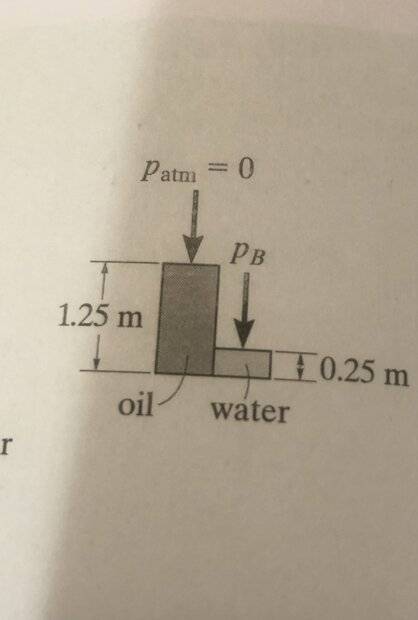
Here is what I am not understanding, why is the pressure due to the water negative and the oil positive, and why are all measurements only made from where the oil meets the water?

i must be missing something really obvious

 

[BvU]

why are all measurements only made from where the oil meets the water?

Because that's how we find the difference between $p_{atm}$ and $p_B$
Going down contributes a positive $\Delta p$ and up a negative $\Delta p$.

One can just as well take the bottom as the turning point: the $\Delta p$ of the extra 1.25 m down is cancelled by $\Delta p$ going up the same 1.25 m

$\$

 

[bigmike94]

Because that's how we find the difference between $p_{atm}$ and $p_B$
Going down contributes a positive $\Delta p$ and up a negative $\Delta p$.

One can just as well take the bottom as the turning point: the $\Delta p$ of the extra 1.25 m down is cancelled by $\Delta p$ going up the same 1.25 m

$\$

Thank you that helped a lot. I attempt the problems quite a bit after I learnt about that method of finding the pressure. Hopefully I’ll remember it

 

[Baluncore]

I think of the problem as moving along a path from the external reference surface to the destination, at point B.
1. Start at the surface with atmospheric pressure. Specify absolute or gauge pressure for the reference.
2. Compute the increasing hydrostatic pressure as you move down through the oil, to the oil-water interface surface.
3. Compute the reducing hydrostatic pressure as you move up through the oil to the destination at point B, on the water-air interface.

 

[Lnewqban]

Here is what I am not understanding, why is the pressure due to the water negative and the oil positive, and why are all measurements only made from where the oil meets the water?

i must be missing something really obvious

This arrangement can be calculated like a U-shaped manometer, if you can imagine the bend located just underneath the central partition.

Please, see:
https://pressbooks.online.ucf.edu/osuniversityphysics/chapter/14-2-measuring-pressure/