Negative radius convention equivalent but not equal?

[nomadreid]

TL;DR

In Wikipedia's description of spherical coordinates, a convention whereby (r,A,B) is equivalent to (-r, -A, pi-B) is presented. It appears that they are not equal, but I guess isomorphic. Wrong?

In
https://en.wikipedia.org/wiki/Spherical_coordinate_system
under the heading
"Unique coordinates"
using the convention (r,P,A) =(radial distance, polar angle, azimuthal angle) ("physicist's convention")
we have
(r,P,A) is equivalent to (-r,-P, π-A).
My three dimensional imagination is horrible, and making a little model out of sticks just ended up in a mess, so I look at the cross-sections:
letting r=5, and either reversing the direction of r then rotating, or vice-versa
letting P=0, then (r,P) ≡(-r,-P)

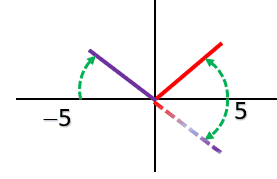
and letting A=0, (r,A) ≡(-r,π-A)

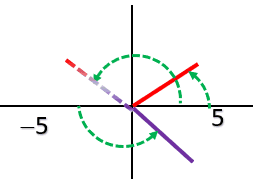
They do not end up at the same place (if I am drawing these correctly), so either I am doing something wrong or what is meant by equivalent is that the systems will be isomorphic, not necessarily equal. However, I would be glad to be corrected.

Thanks for any help.

 

[anuttarasammyak]

Another approach. Translation of Cartesian and polar coordinates are
x=r \sin \theta \cos \phi
y=r \sin \theta \sin \phi
z=r \cos \theta
We can observe the transformation you say, i.e.
r\rightarrow -r,\ \theta\rightarrow -\theta,\ \phi\rightarrow \pi-\phi
in RHS would / would not change LHS.

 

[nomadreid]

anuttarasammyak, thanks, that simplifies the approach tremendously!

Another approach.

My central problem still remains, but now I can state it more succinctly.
Using the conversion above, I get

Unless I have made some mistakes, this again does not end up with the original point. So I remain confused. Where am I going wrong?

 

[Hill]

using the convention (r,P,A) =(radial distance, polar angle, azimuthal angle) ("physicist's convention")
we have
(r,P,A) is equivalent to (-r,-P, π-A).

It rather says that $(-r,-\theta,\phi)$ is equivalent to $(r,\theta,\phi)$.

 

[nomadreid]

The original quote is: "It is convenient in many contexts to use negative radial distances, the convention being (− r , − θ , φ) , which is equivalent to ( r , θ , φ ) for any r, θ, and φ. ​

Moreover , ( r ,− θ , φ ) is equivalent to ( r , θ , φ + 180° ) ."​

Elsewhere in the article it states "Nota bene: the physics convention is followed in this article;"

That is, where θ is the polar angle, and φ is the azimuthal angle. I have merely replaced θ by P and φ by A as a mnemonic for "polar" and "Azimuth". Then I put the two equivalences:
(− r , − θ , φ)≡( r , θ , φ ) & ( r ,− θ , φ ) ≡ ( r , θ , φ + 180° )
into the single
( r , θ , φ )≡(− r , − θ , 180°- φ), i.e., (− r , − θ , π- φ)

I had hoped that this was clear, but I apologize if it was not. (I also apologize for the bold font at the beginning of my posts; I do not know why that happens and why I can't get rid of it.)

Now, with my notation explained, perhaps it will be easier to find where I am making a mistake? Thanks for the patience.

 

[Hill]

The original quote is: "It is convenient in many contexts to use negative radial distances, the convention being (− r , − θ , φ) , which is equivalent to ( r , θ , φ ) for any r, θ, and φ. ​

Moreover , ( r ,− θ , φ ) is equivalent to ( r , θ , φ + 180° ) ."​

Elsewhere in the article it states "Nota bene: the physics convention is followed in this article;"

That is, where θ is the polar angle, and φ is the azimuthal angle. I have merely replaced θ by P and φ by A as a mnemonic for "polar" and "Azimuth". Then I put the two equivalences:
(− r , − θ , φ)≡( r , θ , φ ) & ( r ,− θ , φ ) ≡ ( r , θ , φ + 180° )
into the single
( r , θ , φ )≡(− r , − θ , 180°- φ), i.e., (− r , − θ , π- φ)

I had hoped that this was clear, but I apologize if it was not. (I also apologize for the bold font at the beginning of my posts; I do not know why that happens and why I can't get rid of it.)

Now, with my notation explained, perhaps it will be easier to find where I am making a mistake? Thanks for the patience.

Yes, your notation was clear from the beginning. The mistake I see is here: "( r , θ , φ )≡(− r , − θ , 180°- φ)". How do you get this?

 

[anuttarasammyak]

Unless I have made some mistakes, this again does not end up with the original point. So I remain confused. Where am I going wrong?

You seem all right. We may doubt the description of Wiki.

How about another one

r \rightarrow -r, \ \theta \rightarrow \pi-\theta, \ \phi\rightarrow \pi+\phi

Does it work ?

PS I corrected transformation of $\phi$.

 

[Hill]

You seems all right. How about another one, i.e.
r\rightarrow -r,\ \theta \rightarrow \pi-\theta,\ \phi\rightarrow -\phi

I don't see how they get this: "( r , θ , φ )≡(− r , − θ , 180°- φ)" from this: "(− r , − θ , φ)≡( r , θ , φ )".
?

 

[nomadreid]

Thanks, Hill. You are right, I have made some elementary mistakes. Mainly misplaced negativee signs. But I am still a bit at a loss.

My first mistake was to trust this answer:
https://math.stackexchange.com/ques...-r-be-negative-in-spherical-coordinate-system

So, backing up, and using Wiki to put the two together
( r , θ , φ )≡ (− r , θ , φ+π)

But then I still seem to be making mistakes, but I am not sure where:

Thanks, anuttarasammyak. I'm not sure your version works either

 

[pasmith]

Changing the sign of r is one sign change; we need to operate on \theta and \phi in order to produce one further sign change in each coordinate.

Consider these two maps:

1. \alpha \mapsto \alpha + \pi is equivalent to (\cos \alpha, \sin \alpha) \mapsto (-\cos \alpha, -\sin \alpha).
2. \alpha \mapsto \pi - \alpha is equivalent to (\cos \alpha, \sin \alpha) \mapsto (-\cos \alpha, \sin \alpha).

Note that the second maps [0, \pi] to itself, whereas the first does not. That suggests using the second for \phi and the first for \theta. Hence <br /> (r, \theta, \phi) \mapsto (-r, \theta + \pi, \pi - \phi) should fix (r\sin \phi \cos \theta,r \sin \phi \sin \theta,r\cos \phi).

 

[Hill]

Thanks, Hill. You are right, I have made some elementary mistakes. Mainly misplaced negativee signs. But I am still a bit at a loss.

My first mistake was to trust this answer:
https://math.stackexchange.com/ques...-r-be-negative-in-spherical-coordinate-system

So, backing up, and using Wiki to put the two together
( r , θ , φ )≡ (− r , θ , φ+π)

But then I still seem to be making mistakes, but I am not sure where:

View attachment 340276

Thanks, anuttarasammyak. I'm not sure your version works either

View attachment 340279

I think that both sources you've mentioned are mistaken. It looks to me that the following are equivalent:
$(r,\theta,\phi)=(-r, \pi - \theta,\pi+\phi)=(-r,\pi+\theta,\phi)=(r,-\theta,\pi+\phi)$
Please check.

 

[anuttarasammyak]

How about another one

r→−r, θ→π−θ, ϕ→π+ϕ

Does it work ?

A little explanation. Transformation of angles
\theta \rightarrow \pi -\theta,\ \phi\rightarrow \pi+\phi
make the point on the sphere transffer to the opposite point on the sphere. e.g. North Pole to South Pole.
Regarding it as a vector, multiply -1 to its length brings the point back to the original position.

 

[nomadreid]

Out of the four suggestions of Hill and pasmith, I get one which is suitable. The calculations:

So, unless I have made an error in my calculations (always possible), I think I have the solution to my problem. Thanks for all the patience on the part of all!

 

[Hill]

Out of the four suggestions of Hill and pasmith, I get one which is suitable. The calculations:
View attachment 340325

View attachment 340326

So, unless I have made an error in my calculations (always possible), I think I have the solution to my problem. Thanks for all the patience on the part of all!

I think that C is also "yes":
$y'=(-r)sin(\pi +\theta)sin(\phi)=(-r)(-sin(\theta))sin(\phi)=y$.

 

[nomadreid]

Oops! Thanks very much, Hill. I don't know how that extra negative got in there. So, wonderful bonus!