- #1
chipotleaway
- 174
- 0
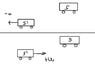
If two events separated in space by Δx occur simultaneously according to an observer S, then the time difference for S' moving at velocity u relative to S is
[tex]\Delta t' = \frac{-u\Delta x}{c^2\sqrt{1-\frac{u^2}{c^2}}}[/tex]
Why is Δt' negative?
[itex]\Delta t' = t'_2 - t'_1[/itex], where [itex]t'_2[/itex] corresponds to time of event 2 and likewise for [itex]t'_1[/itex] and event 1.
At 40:45 in this lecture, he says that this is because the event with the greater coordinate occurs later. But wouldn't this mean that [itex]t'_2>t'_1[/itex] and so Δt' should be positive?
*
Also, is the following statement correct?
Thanks
[tex]\Delta t' = \frac{-u\Delta x}{c^2\sqrt{1-\frac{u^2}{c^2}}}[/tex]
Why is Δt' negative?
[itex]\Delta t' = t'_2 - t'_1[/itex], where [itex]t'_2[/itex] corresponds to time of event 2 and likewise for [itex]t'_1[/itex] and event 1.
At 40:45 in this lecture, he says that this is because the event with the greater coordinate occurs later. But wouldn't this mean that [itex]t'_2>t'_1[/itex] and so Δt' should be positive?
*
Also, is the following statement correct?
When we say such and such events occur at some place and time for S, we have taken into account all relativistic effects, so the events are not necessarily at rest for S (so in original question, S would be traveling at some velocity such that the events are simultaneous, separated by Δx). Therefore when we want to describe the events as seen by S', the velocity u of S' we use is relative to S, and we can only say that it's relative to both S and the events if S is at rest relative to the events.
Thanks
Last edited by a moderator: