Rookie question about proper time

[etotheipi]

I thought I had a decent basic understanding of this stuff, but it turns out I've got quite a lot of gaps. I drew 3 frames, S, S' and S", where S' and S" move at $v_1$ and $v_2$ w.r.t. S in the $x$ direction, and two different paths to a particular event P:

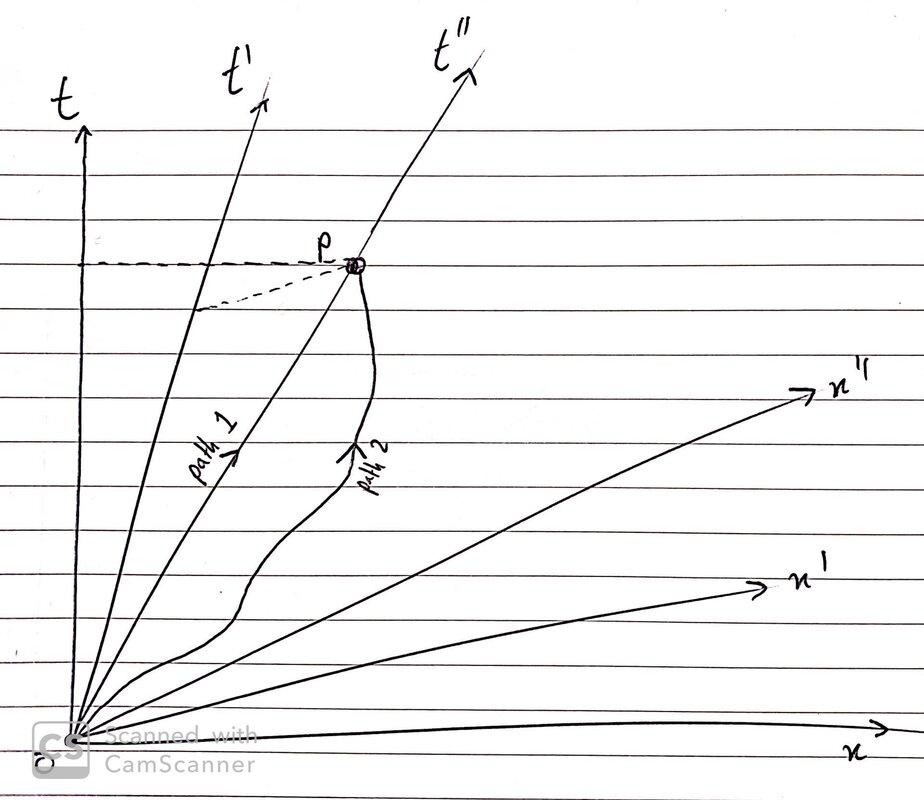
Now the proper time between two events, O and P, is dependent on the path taken through spacetime, and goes something like this with one space dimension $$\Delta \tau = \int_{P} \sqrt{1-\left(\frac{dx}{dt}\right)^2}dt = \int_{P} \frac{dt}{\gamma(t)}$$ and for any given path all different observers will calculate the same $\Delta \tau$. But suppose that between O and P that S" measures a time interval of $\Delta t''$, and we want to figure out what time S measures between those same events. Since O is at $t=t'=t''=0$, we can just look at the times at P. The Lorentz transformations tell me that $$t = \gamma_2 (t'' + v_2 x'')$$ and it follows that $\Delta t = \gamma_2 \Delta t''$.

However, I usually see this quoted as $\Delta t = \gamma_2 \Delta \tau$. The only problem is that $\Delta \tau = \Delta t''$ only if the path is chosen so that the worldline is along the $t''$ axis, and in general there are infinitely many different paths with different $\Delta \tau$ that you could choose between any two events.

So I wondered if someone could clarify, since it would appear to only be valid to say "the time between two events in one frame equals $\gamma$ times the time between the two events in another frame whose time axis is a straight line between those points". Is that right, or is there something snappier/more correct? Thank you, sorry if it's a silly question!

 

[Ibix]

You seem to be deriving the time dilation formula, which does have the restriction that the clock must be stationary in the "moving" frame, yes. Not realising this, and hence applying the formula in a case where the more general Lorentz transforms are needed, is one of the morecommon errors I see here.

 

[etotheipi]

You seem to be deriving the time dilation formula, which does have the restriction that the clock must be stationary in the "moving" frame, yes. Not realising this, and hence applying the formula in a case where the more general Lorentz transforms are needed, is one of the morecommon errors I see here.

And I guess the other restriction would be that there also be no acceleration? Since otherwise you could have a clock stationary at the origin of an accelerating frame, measure the proper time in that frame ($\Delta \tau^2 = \Delta t^2$) and try and use the formula - which would also be wrong.

 

[Ibix]

And I guess the other restriction would be that there also be no acceleration?

Yes - the frames (and hence a clock at rest in one) have to be inertial for you to be using the Lorentz transforms in the first place. The proper time along your accelerated (curvy) path will be lower than the straight path and you'd need to evaluate the integral you gave (which technically you're doing for the straight path too, but it's trivial).

 

[etotheipi]

Yes - the frames (and hence a clock at rest in one) have to be inertial for you to be using the Lorentz transforms in the first place.

Ah okay, understood. Out of interest, what do you do if you want to transform between two frames undergoing, say, uniform relative acceleration?

 

[PeroK]

And I guess the other restriction would be that there also be no acceleration? Since otherwise you could have a clock stationary at the origin of an accelerating frame, measure the proper time in that frame ($\Delta \tau^2 = \Delta t^2$) and try and use the formula - which would also be wrong.

Yes, proper time is always a spacetime interval. That's really something that applies to a particle (rather than a reference frame). If the particle is at rest in some inertial frame, then the spacetime interval in that frame reduces to a coordinate time interval. I.e. if the particle is a clock, then its proper time is coordinate time for that frame.

In all other cases, the proper time of the clock is not the coordinate time.

 

[PeroK]

Ah okay, understood. Out of interest, what do you do if you want to transform between two frames undergoing, say, uniform relative acceleration?

Imagine a spaceship equidistant between two stars, A and B. The ship accelerates very rapidly to relativistic speed towards B. In the original rest frame it is still approximately equidistant from A and B. In the inertial frame of the ship we have length contraction of the distance from A to B. So, the ship is now closer to A and B, despite having accelerated away from A? Hmm!

 

[etotheipi]

Imagine a spaceship equidistant between two stars, A and B. The ship accelerates very rapidly to relativistic speed towards B. In the original rest frame it is still approximately equidistant from A and B. In the inertial frame of the ship we have length contraction of the distance from A to B. So, the ship is now closer to A and B, despite having accelerated away from A? Hmm!

Oh dear... that can't be good?

I suspect the answer is something to do with proper acceleration vs coordinate acceleration, i.e. the captain of the ship (who's definitely getting fired...) holds an accelerometer which tells him he's accelerating toward B, but the coordinate accelerations of A and B w.r.t. the ship are both towards him?

That could be way off...

 

[PeroK]

Oh dear... that can't be good?

I suspect the answer is something to do with proper acceleration vs coordinate acceleration, i.e. the captain of the ship (who's definitely getting fired...) holds an accelerometer which tells him he's accelerating toward B, but the coordinate accelerations of A and B w.r.t. the ship are both towards him?

That could be way off...

Play about with some Lorentz transformations.

 

[etotheipi]

From the Lorentz transformations you can get the relative velocity formulae, and from them you can get $a = \gamma^3 a_0$ if you differentiate again and set one of the rest frames to be the instantaneous rest frame.

If we take the rest frame of the two stars to be S, and the ship S', then I guess the first step is
$$\frac{dv}{dt} = \frac{a_0}{\gamma^3}$$ $$\int \gamma^3 dv = \int a_o dt$$ $$\frac{v}{\sqrt{1-v^2}} = a_0 t$$ $$v = \frac{a_0 t}{\sqrt{1+ a_0^2 t^2}} \implies x = \sqrt{t^2 + \frac{1}{a_0^2}} - \frac{1}{{a_0}^2} + \frac{D}{2}$$ Now the $t$ there's the time in the star frame, whilst we want it in terms of $t'$ in the ship frame? We've also got to figure out the $x'$ of star A/B from that...

 

[PeroK]

It doesn't need to get as complicated as that. The ship starts at rest (relative to the stars) and ends at some inertial speed $v$ moving towards B. You can assume it's still roughly half way between A and B. And, the ship's clock still reads approximately $0$.

Ideally this is instantaneous acceleration, but hypotehtically you can get as close to this as you need.

To help you conceptualise this, imagine the ship accelerates at a space station - half way between A and B. The whole acceleration process takes (approximately) zero time and zero distance. The ship is still at the space station, moving at speed $v$, it's clock read $t=0$, which agrees with the space station clock (which is synchronised with clocks at A and B).

In the new (moving) ship frame (make this the primed frame) what are the coordinates of the events at A and B at time $t =0$? These are the events at A and B when the acceleration began (and ended) in the original rest frame.

 

[etotheipi]

In the new (moving) ship frame (make this the primed frame) what are the coordinates of the events at A and B at time $t =0$? These are the events at A and B when the acceleration began (and ended) in the original rest frame.

In that case I think it would just be $x'_A = -\frac{D}{2\gamma}$ and $x'_B = \frac{D}{2\gamma}$; so A definitely gets closer!

 

[PeroK]

In that case I think it would just be $x'_A = -\frac{D}{2\gamma}$ and $x'_B = \frac{D}{2\gamma}$; so A definitely gets closer!

Yes, okay, but what about the time coordinate?

 

[etotheipi]

Ah okay, yes I forgot that in SR you need to specify that too...

$t' = \frac{\gamma vD}{2}$ for the event at A, and $t' = -\frac{\gamma vD}{2}$ for the event at B.

I think I should draw a spacetime diagram...

 

[PeroK]

In that case I think it would just be $x'_A = -\frac{D}{2\gamma}$ and $x'_B = \frac{D}{2\gamma}$; so A definitely gets closer!

Sorry, I didn't look at this carefully. This isn't correct. The times are correct.

 

[etotheipi]

$\gamma$'s on top? Whoops... . Here's the promised diagram:

 

[PeroK]

In any case, the point was that trying to put different inertial frames together doesn't lead to satisfactory global coordinate system. In this case, the event at B and $t=0$ in the original rest frame, tends to move back in time, according to instantaneous inertial frames associated with the accelerating ship. And you end up the same event (a clock at B reading $t=0$) with two coordinates in the ship frame: $(0, \frac D 2)$ and $(-\frac{\gamma v D}{2}, \frac{\gamma D}{2})$.

Alternatively, if you let some time pass, then B gets to $\frac D \gamma$, as expected, at $t' = 0$. But then the clock at $B$ shows some time $\frac{vD}{2}$ and you've missed some events in the rocket frame.

Either way, you either end up with duplicate coordinates or missing events.

 

[etotheipi]

And you end up the same event (a clock at B reading $t=0$) with two coordinates in the ship frame: $(0, \frac D 2)$ and $(-\frac{\gamma v D}{2}, \frac{\gamma D}{2})$.

Alternatively, if you let some time pass, then B gets to $\frac D \gamma$, as expected, at $t' = 0$. But then the clock at $B$ shows some time $\frac{vD}{2}$ and you've missed some events in the rocket frame.

Either way, you either end up with duplicate coordinates or missing events.

It's times like now I wish Newton had it right all along...

I think I understand your point; accelerations are a little more nuanced than I thought. I think I'm just going to have to trust the maths on this one... since it's pretty odd!

 

[PeroK]

It's times like now I wish Newton had it right all along...

I think I understand your point; accelerations are a little more nuanced than I thought. I think I'm just going to have to trust the maths on this one... since it's pretty odd!

The point is that there is not a super-Lorentz transformation that, say, picks up accelerating reference frames. One way to look at this, thinking ahead to GR, is to focus on local reference frames that represent what someone measures and appropriate global reference frames (or coordinate systems) to study a problem. In this case, you don't need to attribute coordinates to every event in the ship's accelerating frame. It's enough to predict what the ship measures: i.e. the set of local events.

Generally, you are more constrained in SR to stick to analysis in inertial frames than you are in Newton, where you just need to account for ficticious forces. This doesn't stop you analysing arbitrary motion - you just do that using an inertial reference frame - but it gets complicated if you step out of the comfort of the set of inertial reference frames.

 

[etotheipi]

So acceleration's fair game, just don't transform into the frame? Blast, I think Morin's limerick obsession has been rubbing off...

 

[Ibix]

So acceleration's fair game, just don't transform into the frame? Blast, I think Morin's limerick obsession has been rubbing off...

The problem is that there isn't a single "natural" process to define simultaneity in non-inertial frames. That makes them a lot more complicated than inertial frames. There are ways around this, but they generally involve invoking most of the maths of GR. You never actually need to use a non-inertial frame in SR, so just ignoring them until you've covered GR is a workable strategy.