No. of spinless particles in the left half of a box

[Pushoam]

Homework Statement

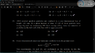
How to solve question no. 35?

Homework Equations

The Attempt at a Solution

Since the particle is spinless, spin = 0 , this means that the particle is a boson.
Applying Bose - Einstein distribution function,
$f(E) = \frac1 { e^{\beta ( E - \mu)} -1}$
I can get the value of $\beta$ and $\mu$ [as this distribution function tells us the no. of particles having the energy E of a given system.
Since I have LHS for two given values of E, I have 2 eqns. and hence I can determine $\beta$ and $\mu$ .
Now, what to do?
How to connect this with the given information in question?

 

[DrClaude]

Applying Bose - Einstein distribution function,
$f(E) = \frac1 { e^{\beta ( E - \mu)} -1}$

You have a system with a fixed energy, not a fixed temperature, hence to BE distribution does not apply. Start by considering the eigenstates of a particle in a box.

 

[Pushoam]

You have a system with a fixed energy, not a fixed temperature, hence to BE distribution does not apply. Start by considering the eigenstates of a particle in a box.

The eigen energy of a particle in a box is
$E_n = \frac{ n^2 h^2}{2 m a^2} = n^2 \epsilon_0$
This gives that the particles are in the states n =2,15.
Do I have to calculate the probability of getting a particle with energy $E_2 ~ and~ E_{15}$ each in the left half region and then I will multiply the probabililty with 1000 and add the two no.?

 

[DrClaude]

Do I have to calculate the probability of getting a particle with energy $E_2 ~ and~ E_{15}$ each in the left half region and then I will multiply the probabililty with 1000 and add the two no.?

Basically yes, assuming that the observation time is chosen randomly (or consider the result "on average").

 

[Pushoam]

Basically yes, assuming that the observation time is chosen randomly (or consider the result "on average").

I didn't get the assumption. Why do we need the assuption?

 

[DrClaude]

I didn't get the assumption. Why do we need the assuption?

Because a superposition of stationary states of different energies is not itself a stationary state. The particles will be sloshing from left to right.

 

[sayakd]

i calculated the probability of finding a particle on the left half of the box, and it is always 1/2 for a stationary state, for all n..
so, for the particles with energy 4e, the no of particles on the left half 100/2 = 50, for 225e, 900/2 = 450, total 500..

best of luck for the TIFR GS btw..

 

[Pushoam]

Thanks.

 

[Pushoam]

i calculated the probability of finding a particle on the left half of the box, and it is always 1/2 for a stationary state, for all n..

Is the probability of finding the particle between $x_i and x_f$ for 1 D box $\frac { x_f - x_i} { L}$, where L is the length of the box?

I am not caclculating it. I just want to see it this way if it is so.

 

[sayakd]

I don't know the closed way to represent the probability, what I did was integration of psi* multiplied by psi with the limit - L to 0,where psi is the normalized wavefunction of 1d potential box.. 2L is the length of the box..