Nodal Analysis and Two Dependent Current Sources

[Young_Scientist23]

TL;DR

The topis is related to the usage of nodal analysis in the circuit having two dependent current sources.

Hello,

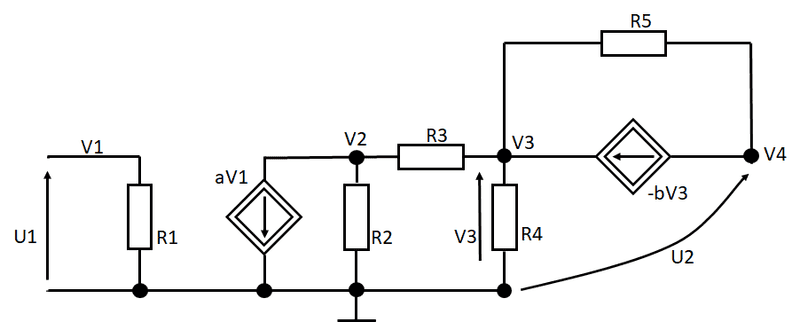
I came up with a circuit that has two independent voltage-controlled current sources. I want to calculate voltage gain: $G_{U} = \frac{U_{2}}{U_{1}}$. Moreover, I want to practice the nodal method at the same time. Below I'm sending schematic with marked nodes V1, V2, V3 and V4.

I derived the circuit conductance matrix G and I want to calculate the mentioned gain by determining the determinants of the matrix i.e.:

$$U_{1} = V_{1} = \frac{\Delta_{1}}{\Delta}$$
$$U_{2} = V_{4} = \frac{\Delta_{4}}{\Delta}$$

Unfortunately, the determinants are zero and I don't know why. Can you suggest what I may be doing wrong? I'm sending derived matrix.

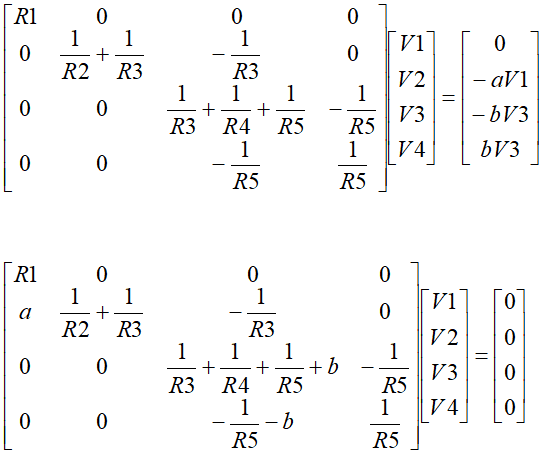
Regards,
Tom

 

[The Electrician]

You have a couple of mistakes in your conductance matrix. Also you need a source of voltage driving the input before you can have any output. If the right hand column vector is all zeroes, when you use that to replace one of the columns in the conductance matrix you get a determinant of zero. Include a driving source Vs as I've shown. You don't need to calculate the voltage at V1 since that will be a given, namely Vs.

Finish working it out and post your result. If you're interested, I'll show you a shortcut method to get the voltage gain expression.

 

[Young_Scientist23]

You have a couple of mistakes in your conductance matrix. Also you need a source of voltage driving the input before you can have any output. If the right hand column vector is all zeroes, when you use that to replace one of the columns in the conductance matrix you get a determinant of zero. Include a driving source Vs as I've shown. You don't need to calculate the voltage at V1 since that will be a given, namely Vs.

View attachment 328953
Finish working it out and post your result. If you're interested, I'll show you a shortcut method to get the voltage gain expression.

Thank you for the response and correction. Yep, I've made mistakes in G matrix (those typos have been made during writting matrices for this forum). I calculated $\Delta_{1}$ and $\Delta_{2}$ according to your suggestions: $$\Delta_{1} = \frac{Vs(R2+R3+R4)}{R2R3R4R5}$$
$$\Delta_{2} = - \frac{aVs(bR5+1)}{R3R5}$$
what gives
$$V_{1} = VsR1$$
$$V_{4} = - \frac{aVsR1R2R4(bR5+1)}{R2+R3+R4}$$

and finally voltage gain is:
$$G_{U} = - \frac{aR2R4(bR5+1)}{R2+R3+R4}$$

I'm confused due to "current values vector", because You just add voltage Vs there. It is correct ? We can treat this as some kind of "constant term"/any parameter nor variable direcly related to current ? I was quite confused when I saw that (why is not $\frac{Vs}{R1}$.

If you're interested, I'll show you a shortcut method to get the voltage gain expression.

I'll be appriciate if you can tell something more about this shorcut :)

Regards,
Tom

 

[The Electrician]

You are correct to be skeptical of the Vs variable; it should just be a current Is. If you use Is in all your calculations, you will get the result you already got.

To do the shortcut, form the admittance (conductance) matrix, invert it to form the impedance matrix. The voltage gain from node j to node k is given by the ratio of the (k,j) element of the impedance matrix to the (j,j) element. In other words, Gu = Z(k,j)/Z(j,j) = Z(4,1)/Z(1,1) in your case.

This works for any pair of nodes. It will give you the reverse voltage gain from node 4 to node 1, or from node 2 to node 3. It assumes that the stimulus applied to the input node is a voltage source.

 

[Young_Scientist23]

Thank you for explanation !