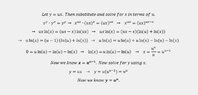The answer is: $(x,y) = (0,0)$ or $(k^{k-1},k^k)$, where $k \in \mathbb{N}$.
Let $(x,y)$ be a rational nonzero solution. Consider a substitution $t = \frac{y}{x}$.
Then $x^{tx}(tx)^x = (tx)^{tx}$ or $x = t^{t-1}$. If $t-1 = k$ then $x = (k+1)^k$. Let us show, that $k$ is a natural number. Take $x=\frac{m}{n}$ and $k = \frac{p}{q}$ where both fractions are irreducible:
$gcd(m,n) = 1$ and $gcd(p,q) = 1$. Then our equation becomes:
$$m^qq^p = n^q(p+q)^p$$
Since $m$ and $n$ are coprimes, $n^q|q^p$ and since $p$ and $q$ are coprimes, $gcd((p+q)^p,q^p) = (gcd(p+q,q))^p = gcd(p,q)^p = 1$. Therefore, $q^p|n^q$, and as a result $q^p = n^q$. Suppose, that $q > 1$. Then in the prime decomposition of $q^p$ each factor has a power divisible by both $p$ and $q$, and hence divisible by $pq$. Therefore, in the prime decomposition of $q$ each factor has a power divisible by $q$. But this is a contradiction, since $q < 2^q$. Thus, $q = 1$ and $x = k^{k-1}$ and $y = k^k$. Straightforward check shows, that $(0,0)$ and $(k^{k-1},k^k)$ are solutions. Done.