Noob question about lorentz factor

[Waaaaaaaa]

Hello

So i saw this video on youtube explaining some basics of general relativity and they used example with 2 rockets moving paralelly with laser pointed from rocket A to mirror on rocket B.
Heres my picture of it :D

Where we are stationary observer watching those two rockets A and B move paralelly.
Here when we consider speed of light as maximal its possible to deduce lorentz factor as factor of speed at which our light beam Y closes from A to B and then back and everything looks fine and works great. But if i try to imagine situation where those two ships do not move paralelly but one after the other.. like on this great picture..

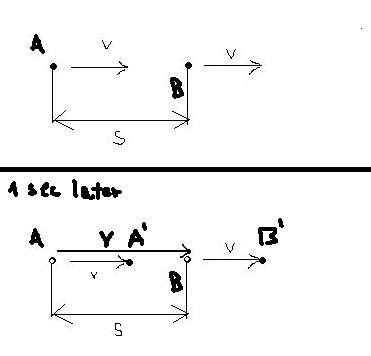
Everything just breaks down in my head... let's say velocity of both rockets is c/2 [m/s]
their distance s= c [m] ( one light second)
So i have a few questions and just to be sure I am not making some very bad assumptions, here is what i think must happen :
1] from our (stationary) point of view the light beam will reach ship B in t=2 seconds
2] from our point of view the light beam will reflect back to ship A and reach it in t=2.66 seconds

lets say on ship B is machine which every 0.1 second ejects a signal flag from the ship.
The flag will be green if no light beam hit the mirror and red if ligh beam has allready hit the mirror.
now let's go on board of ship A and beam that light on to them.. now we are 1.9 seconds after beam and they are still pushing out green flags,now they switch, only 7 flags comes out red and then there's our light beam... So what am i missing here ?? I mean the light could not travel different speed on its way back. Also the number of flags may be different due to some time dilatation but i don't think that could hamper the experiment at v= c/2 which is lorentz factor 1.15

Dont bash me pls
Thanks for answers

 

[Simon Bridge]

The observer in the rocket will observe the same number of flags as the observer at the spaceport, but they will disagree about how much time elapses between the flags. There will be 0.1s between flags for one observer and 0.115s between flags for the other.

 

[Waaaaaaaa]

Ok, but how many of the flags is green ? I mean from the point of rocket A the rocket B is stationary. Yet the number of flags indicate that light travels much longer on its way to rocket B than on its way back. Which is contradiction to general relativity is it not?

 

[ghwellsjr]

Why don't you give us the link to the video?

 

[Waaaaaaaa]

Why don't you give us the link to the video?

The video doesn't cover this. Its just a scenario i thought about. My issue is that according to general relativity speed of light should be same to all observers. Yet if my example is to be correct there would be evidence on board rocket A that light traveled much slowly on its way to rocket B. And if let's say number of green and red flags had to be same, then from point of stationary observer (ie starbase) machines on rocket B would have to start sending red flags about 0.6 seconds earlier than light could (at light speed observed from that starbase) reach that rocket ... which mean they would have to see 0.6 seconds into the future... which is quite a feat for some fototranzistor.

 

[Waaaaaaaa]

I found my answer here http://www.youtube.com/watch?v=202fU9qIVK4&feature=relmfu
I didnt know how the length contraction fits in. The first picture fits because there is no length contraction in direction of the beam.

 

[Simon Bridge]

You have to be real careful about who is measuring what.