Undergrad Normal Modes: Finding Eigenfrequencies

Click For Summary
To find the eigenfrequencies corresponding to the given eigenvectors of a system with three particles, one must typically solve the characteristic equation derived from the system's dynamical matrix. The eigenfrequencies are determined by the square roots of the eigenvalues obtained from this matrix. The discussion highlights a lack of clarity in the source material, which provided eigenfrequencies without explaining the derivation process. This has led to confusion about the method to calculate them. Understanding the relationship between eigenvectors and eigenfrequencies is crucial for analyzing the system's motion.
Sum Guy
Messages
21
Reaction score
1
If I have a system where the following is found to describe the motion of three particles:

1zyzm8z.png

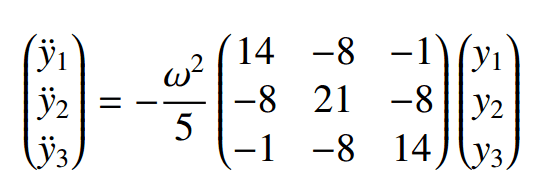
The normal modes of the system are given by the following eigenvectors: $$(1,0,-1), (1,1,1), (1,-2,1)$$
How can I find the corresponding eigenfrequencies? It should be simple... What am I missing?
 
Physics news on Phys.org
Is this for schoolwork?
 
berkeman said:
Is this for schoolwork?
This is something I found in a pdf online where it simply asserted what the eigenfrequencies were... and not how to find them.
 
  • Like
Likes berkeman

Thread 'Reference frames, center of rotation, etc'

Topic about reference frames, center of rotation, postion of origin etc Comoving ref. frame is frame that is attached to moving object, does that mean, in that frame translation and rotation of object is zero, because origin and axes(x,y,z) are fixed to object? Is it same if you place origin of frame at object center of mass or at object tail? What type of comoving frame exist? What is lab frame? If we talk about center of rotation do we always need to specified from what frame we observe?
View full post »

Similar threads

Undergrad Error tolerant normal mode frequency
  • · Replies 7 ·
Replies
7
Views
2K
Undergrad Normal modes of vibration from the total energy
  • · Replies 3 ·
Replies
3
Views
1K
Small oscillations: How to find normal modes?
  • · Replies 3 ·
Replies
3
Views
3K
Analysing the Normal Modes and Dynamics of a Cluster of Atoms
  • · Replies 1 ·
Replies
1
Views
1K
Understanding solution to equations of motion of n coupled oscillators
  • · Replies 4 ·
Replies
4
Views
2K
Coupled oscillators -- period of normal modes
  • · Replies 11 ·
Replies
11
Views
2K
Graduate Equipartition theorem and Coupled harmonic oscillator system
  • · Replies 3 ·
Replies
3
Views
2K
Normal modes of four coupled oscillating masses (Kleppner and Kolenkow)
  • · Replies 4 ·
Replies
4
Views
2K
Finding the normal modes for a oscillating system
  • · Replies 4 ·
Replies
4
Views
2K
Can Eigenfrequencies Explain Oscillatory Behavior in this Dynamical System?
  • · Replies 3 ·
Replies
3
Views
3K